Using the Squeeze Theorem to Find a Limit

Use the Squeeze Theorem to find \(\lim\limits_{x\rightarrow 0}\left( x\sin \dfrac{1}{x}\right)\).

Solution If \(x\neq 0\), then \(\sin \dfrac{1}{x}\) is defined. We seek two functions that “squeeze” \(y=x\sin \dfrac{1}{x}\) near \(0.\) Since \(-1\leq \sin x\leq 1\) for all \(x,\) we begin with the inequality \begin{equation*} \left\vert \sin \dfrac{1}{x}\right\vert \leq 1\qquad x\neq 0 \end{equation*}

Since \(x\neq 0\) and we seek to squeeze \(x\sin \dfrac{1}{x},\) we multiply both sides of the inequality by \(\vert x\vert ,\) \(x\neq 0.\) Since \(\vert x\vert >0,\) the direction of the inequality is preserved. Note that if we multiply \(\left\vert \sin \dfrac{1}{x}\right\vert \leq 1\) by \(x,\) we would not know whether the inequality symbol would remain the same or be reversed since we do not know whether \(x>0\) or \(x\lt 0.\) \begin{equation*} \begin{array}{r@{\qquad}ll} |x|\left\vert \sin \dfrac{1}{x}\right\vert \leq |x| & & {\color{#0066A7}{\hbox{Multiply both sides by \(\vert x \vert >0\).}}} \\[12pt] \left\vert x\sin \dfrac{1}{x}\right\vert \leq |x| & & {\color{#0066A7}{{|a|\cdot |b| = |a\,b|}.}} \\[11pt] -\vert x\vert \leq x\sin \dfrac{1}{x}\leq |x| & & {\color{#0066A7}{\vert a\vert\,{\leq}\,b\hbox{ is equivalent to } {-b\leq a\leq b.}}} \end{array} \end{equation*}

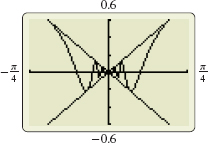
Now use the Squeeze Theorem with \(f(x) = - |x|\), \(g(x) = x\sin \dfrac{1}{x}\), and \(h(x) = |x|\). Since \(f(x)\leq g(x)\leq h(x)\) and \begin{equation*} \lim_{x\rightarrow 0}f(x)=\lim_{x\rightarrow 0}(-|x|)=0\qquad \hbox{and}\qquad \lim_{x\rightarrow 0}h(x)=\lim_{x\rightarrow 0}\vert x\vert =0 \end{equation*}

it follows that \[ \lim_{x\rightarrow 0}g(x)=\lim_{x\rightarrow 0}\left( x\cdot \sin \frac{1}{x} \right) =0 \]