Find all points on the graph of $f(x) =x+\sin x$ where the tangent line is horizontal.

Solution Since tangent lines are horizontal at points on the graph of $f$ where $f^\prime (x) =0,$ we begin by finding $f^\prime$: $$f^\prime (x) =1+\cos x$$ Now we solve the equation $f^\prime (x) =0.$ $$\begin{array}{rcl@{\qquad}l} f^\prime (x) &=& 1+\cos x=0 \\[0pt] \cos x &=& -1 \\[0pt] x &=& (2k+1) \pi &\hbox{where }{k}\hbox{ is an integer} \end{array}$$

188

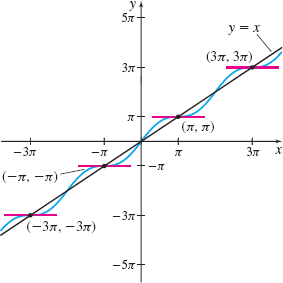
Figure 27 $f(x)=x+\sin x$

The graph of $f( x) =x+\sin x$ has a horizontal tangent line at each of the points $( ( 2k+1) \pi , ( 2k+1) \pi )$, $k$ an integer. See Figure 27 for the graph of $f$ with the horizontal tangent lines marked. Notice that each of the points with a horizontal tangent line lies on the line $y=x.$