Figure

EXAMPLE 6Analyzing Simple Harmonic Motion

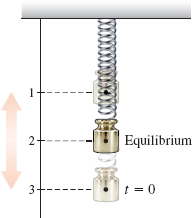
An object hangs on a spring, making it 2 m long in its equilibrium position. See Figure 28. If the object is pulled down 1 m and released, it will oscillate up and down. The length $l$ of the spring after $t$ seconds is modeled by the function $l( t) =2+\cos t$ .

Figure 28

(a) How does the length of the spring vary?
(b) Find the velocity of the object.
(c) At what position is the speed of the object a maximum?
(d) Find the acceleration of the object.
(e) At what position is the acceleration equal to 0?

Solution

Since $l(t) =2+\cos t$ and $-1 ≤ \cos t ≤ 1,$ the length of the spring oscillates between 1 m and 3 m.
The velocity $v$ of the object is $v=l' ( t) =\dfrac{d}{dt}\left( 2+\cos t\right) =-\sin t$
Speed is the magnitude of velocity. Since $v=-\sin t,$ the speed of the object is $\left\vert v\right\vert =\left\vert -\sin t\right\vert =\left\vert \sin t\right\vert$ . Since $-1 ≤ \sin t ≤ 1,$ the object moves the fastest when $\left\vert v\right\vert =\left\vert \sin t\right\vert =1.$ This occurs when $\sin t=\pm 1$ or, equivalently, when $\cos t=0.$ So, the speed is a maximum when $l( t) =2,$ that is, when the spring is at the equilibrium position.
The acceleration $a$ of the object is given by $a=l'' ( t) =\dfrac{d}{dt}l' (t)=\dfrac{d}{dt} ( -\sin t) =-\cos t$
Since $a=-\cos t,$ the acceleration is zero when $\cos t=0.$ This occurs when $l( t) =2,$ that is, when the spring is at the equilibrium position. At this time, the speed is maximum.