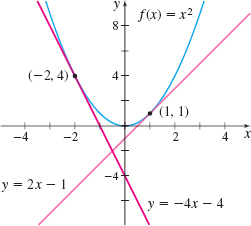
Finding an Equation of the Tangent Line to the Graph of \(f(x) =x^{2}\)

1. Find the slope of the tangent line to the graph of \(f(x) =x^{2}\) at \(c=1\) and at \(c=\) \(-2\).
2. Use the results from (a) to find an equation of the tangent lines when \(c=1\) and \(c=-2\).
3. Graph \(f\) and the two tangent lines on the same set of axes.

Solution

(a) At \(c=1\), the slope of the tangent line is \[ \begin{eqnarray*} f^\prime (1) &=&\lim\limits_{x\rightarrow 1}\dfrac{f(x) -f(1) }{x-1} \underset{\underset{\color{#0066A7}{f( x) =x^{2}}}{\color{#0066A7}{\uparrow }}}{=} \lim\limits_{x\rightarrow 1}\dfrac{x^{2}-1}{x-1} =\lim\limits_{x\rightarrow 1}\dfrac{( x-1) ( x+1) }{x-1}=\lim\limits_{x\rightarrow 1}( x+1) =2 \end{eqnarray*} \]

At \(c=-2\), the slope of the tangent line is \begin{eqnarray*} f^\prime ( -2) &=&\lim\limits_{x\rightarrow -2}\dfrac{ f( x) -f( -2) }{x-(-2)}=\lim\limits_{x\rightarrow -2} \dfrac{x^{2}-( -2) ^{2}}{x+2}=\lim\limits_{x\rightarrow -2}\dfrac{ x^{2}-4}{x+2}\\[11pt] &=&\lim\limits_{x\rightarrow -2}( x-2) =-4 \end{eqnarray*}

(b) We use the results from (a) and the point-slope form of an equation of a line to obtain equations of the tangent lines. An equation of the tangent line containing the point \((1, f(1)) =(1,1) \) is \begin{eqnarray*} \begin{array}{rl@{\qquad}l} y-f(1) &= f^\prime (1) ( x-1) & {\color{#0066A7}{\hbox{Point-slope form of an equation of the tangent line.}}}\\[5pt] y-1 &= 2( x-1) & {\color{#0066A7}{\hbox{\(f(1) = 1;\quad f^\prime(1) =2.\)}}} \\[5pt] y &= 2x-1 & {\color{#0066A7}{\hbox{Simplify.}}} \end{array} \end{eqnarray*}

149

An equation of the tangent line containing the point \(( -2, f( -2)) =(-2,4) \) is \begin{eqnarray*} \begin{array}{rl@{\qquad}l} y-f( -2) &= f^\prime ( -2) [x-( -2)] \\[5pt] y-4 &=-4\cdot (x+2) & {\color{#0066A7}{\hbox{\(f(-2) = 4; \quad f^\prime (-2) =-4\)}}} \\[5pt] y &=-4x-4 \end{array} \end{eqnarray*}

(c) The graph of \(f\) and the two tangent lines are shown in Figure 5.