Finding the Derivative Function

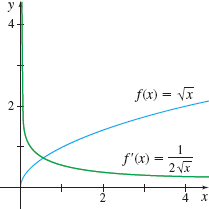
Differentiate \(f(x)=\sqrt{x}\) and determine the domain of \(f^\prime\).

Solution The domain of \(f\) is \(\{x|x ≥ 0\}\). To find the derivative of \(f\), we use form (3). Then \[ f^\prime ( x) =\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{\sqrt{ x+h}-\sqrt{x}}{h} \]

We rationalize the numerator to find the limit. \begin{eqnarray*} f^\prime ( x) &=&\lim\limits_{h\rightarrow 0}\left[ \dfrac{\sqrt{ x+h}-\sqrt{x}}{h}\cdot \dfrac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x} } \right] =\lim\limits_{h\rightarrow 0}\dfrac{( x+h) -x}{ h( \sqrt{x+h}+\sqrt{x}) } \\[5pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{h}{h( \sqrt{x+h}+\sqrt{x}) } =\lim\limits_{h\rightarrow 0}\dfrac{1}{\sqrt{x+h}+\sqrt{x}}=\dfrac{1}{2\sqrt{ x}} \end{eqnarray*}

The limit does not exist when \(x=0.\) But for all other \(x\) in the domain of \(f\), the limit does exist. So, the domain of the derivative function \(f^\prime (x) =\dfrac{1}{2\sqrt{x}}\) is \(\{ x|x>0\}\).