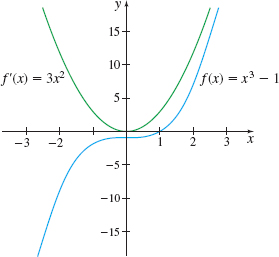
Graphing a Function and Its Derivative

Find \(f^\prime\) if \(f( x) =x^{3}-1\). Then graph \(y=f( x)\) and \(y=f^\prime ( x)\) on the same set of coordinate axes.

Solution \(f( x) =x^{3}-1\) so \[ f( x+h) =( x+h) ^{3}-1=x^{3}+3hx^{2}+3h^{2}x+h^{3}-1 \] Using form (3), we find \begin{eqnarray*} f^\prime ( x) &=&\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{( x^{3}+3hx^{2}+3h^{2}x+h^{3}-1) -( x^{3}-1) }{h}\\[7pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{3hx^{2}+3h^{2}x+h^{3}}{h} =\lim\limits_{h\rightarrow 0}\dfrac{h( 3x^{2}+3hx+h^{2}) }{h}\\[7pt] &=&\lim\limits_{h\rightarrow 0}( 3x^{2}{+}3hx{+}h^{2}) =3x^{2} \end{eqnarray*}

The graphs of \(f\) and \(f^\prime\) are shown in Figure 9.