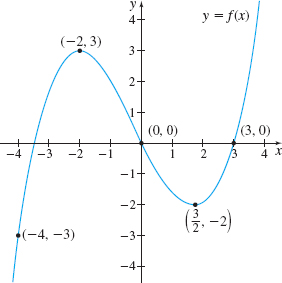
Graphing the Derivative Function

Use the graph of the function \(y=\) \(f(x)\), shown in Figure 11, to sketch the graph of the derivative function \(y=f^\prime (x)\).

Solution We begin by drawing tangent lines to the graph of \(f\) at the points shown in Figure 11. See the graph at the top of Figure 12. At the points \((-2, 3)\) and \(\left(\dfrac{3}{2},-2\right)\) the tangent lines are horizontal, so their slopes are 0. This means \(f^\prime ( -2) =0\) and \(f^\prime \left(\dfrac{3}{2}\right) =0,\) so the points \((-2, 0)\) and \(\left(\dfrac{3}{2},0\right)\) are on the graph of the derivative function. Now we estimate the slope of the tangent lines at the other selected points. For example, at the point \(( -4,-3) .\) the slope of the tangent line is positive and the line is rather steep. We estimate the slope to be close to \(6,\) and we plot the point \((-4,6)\) on the bottom graph of Figure 12. Continue the process and then connect the points with a smooth curve.