Solution (a) $$\begin{eqnarray*} f^\prime ( x) &=&\dfrac{d}{dx}( 2x^{4}-6x^{2}+2x-3) {=} \dfrac{d}{dx}( 2x^{4}) -\dfrac{d}{dx}( 6x^{2}) +\dfrac{d}{dx} ( 2x) -\dfrac{d}{dx}3 \\[-6.4pt] &&\hspace{4.85pc}\underset{{\color{#0066A7}{\text{Sum & Difference Rules}}}}{\color{#0066A7}{\uparrow }}\\[-6.4pt] &{=}& 2\cdot \dfrac{d}{dx}x^{4}-6\cdot \dfrac{d}{dx}x^{2}+2\cdot \dfrac{d}{dx}x-0 \\[-6.4pt] &&\hspace{-3.15pc}\underset{{\color{#0066A7}{\text{Constant Multiple Rule}}}}{\color{#0066A7}{\uparrow }}\\ &{=}& 2\cdot 4x^{3}-6\cdot 2x+2\cdot 1 {=} 8x^{3}-12x+2\\[-6.4pt] &&\hspace{-3.7pc}\hspace{1pc}\underset{\color{#0066A7}{\text{Simple Power Rule}}}{\color{#0066A7}{\uparrow }}\hspace{4.4pc}\underset{{\color{#0066A7}{\text{Simplify}}}}{\color{#0066A7}{\uparrow }} \end{eqnarray*}$$

(b) $f^\prime (2) =8( 2)^{3} -12(2) +2=64-24+2=42$.

(c) The slope of the tangent line at the point (1, −5) equals $f′(1)$. $$f^\prime (1) =8( 1)^{3} -12(1) +2=8-12+2=-2$$

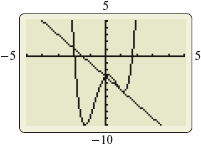
Figure 22 $f(x) = 2x^4 -6 x^2 +2x-3$

(d) We use the point-slope form of an equation of a line to find an equation of the tangent line at $(1,-5)$. $$\begin{eqnarray*} y-( -5) &=&-2( x-1) \\ y &=&-2( x-1) -5=-2x+2-5=-2x-3 \end{eqnarray*}$$

The line $y=-2x-3$ is tangent to the graph of $f( x) =2x^{4}-6x^{2}+2x-3$ at the point $(1, -5)$.

(e) The graphs of $f$ and the tangent line to $f$ at $(1, -5)$ are shown in Figure 22.