Solving Equations and Inequalities Involving Derivatives

  1. Find the points on the graph of \(f( x) =4x^{3}-12x^{2}+2\), where \(f\) has a horizontal tangent line.
  2. Where is \(f^\prime (x)>0\)? Where is \(f'(x) < 0\)?

Solution (a) The slope of a horizontal tangent line is 0. Since the derivative of \(f\) equals the slope of the tangent line, we need to find the numbers \(x\) for which \(f^\prime ( x) =0\). \[ \begin{eqnarray*} f^\prime ( x) &=& 12x^{2}-24x = 12x (x-2) \\ 12x ( x-2 ) &=& 0 & {\color{#0066A7}{\hbox{\(f^{\,\prime} ( x ) =0.\)}}} \\ x &=&0\hbox{ or }x=2 & {\color{#0066A7}{\hbox{Solve.}}} \end{eqnarray*} \]

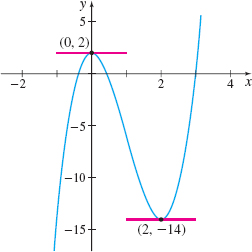
Figure 23 \(f(x) = 4x^3 -12x^2 +2\)

At the points \(( 0,f( 0) ) =( 0,2)\) and \(( 2,f(2) ) =( 2,-14)\), the graph of the function \(f( x) =4x^{3}-12x^{2}+2\) has a horizontal tangent line.

(b) Since \(f^\prime(x)=12x (x-2)\) and we want to solve the inequalities \(f^\prime(x)>0\) and \(f^\prime(x) < 0\), we use the zeros of \(f^\prime\), 0 and 2, and form a table using the intervals (\(-\infty,0\)), (0,2), and (\(2, \infty)\).

TABLE 2
Interval \((-\infty,0)\) (\(0,2\)) (\(2, \infty)\)
Sign of \(f'(x) = 12x(x-2)\) Positive Negative Positive

We conclude \(f'(x)>0\) on \((-\infty,0) \cup (2,\infty)\) and \(f'(x) < 0\) on \((0,2)\),