Analyzing Vertical Motion

A ball is propelled vertically upward from the ground with an initial velocity of 29.4 meters per second. The height \(s\) (in meters) of the ball above the ground is approximately \(s=s( t) =-4.9t^{2}+29.4t\), where \(t\) is the number of seconds that elapse from the moment the ball is released.

1. What is the velocity of the ball at time \(t\)? What is its velocity at \(t=1\)second?
2. When will the ball reach its maximum height?
3. What is the maximum height the ball reaches?
4. What is the acceleration of the ball at any time \(t\)?
5. How long is the ball in the air?
6. What is the velocity of the ball upon impact with the ground?
7. What is the total distance traveled by the ball?

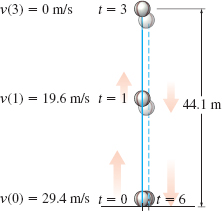
Solution (a) Since \(s=-4.9t^{2}+29.4t\), then \[ \begin{eqnarray*} v&=&v( t) ={\dfrac{ds}{dt}}=-9.8t+29.4\\[5pt] v(1) &=&-9.8+29.4=19.6 \end{eqnarray*} \]

At \(t=1\), the velocity of the ball is \(19.6m/s\).

180

(b) The ball reaches its maximum height when \(v( t) =0\).\[ \begin{eqnarray*} v( t) &=&-9.8t+29.4=0 \\ 9.8t &=& 29.4 \\ t &=&3 \end{eqnarray*} \]

The ball reaches its maximum height after 3 seconds.

(c) The maximum height is \[ s=s(3) =-4.9(3^{2})+29.4(3)=44.1 \]

The maximum height of the ball is \(44.1\) m.

(d) The acceleration of the ball at any time \(t\) is \[ a=a( t) ={\dfrac{d^{2}s}{dt^{2}}}=\dfrac{dv}{dt}=\dfrac{d}{dt}( -9.8t+29.4) =-9.8m/s^{2} \]

(e) There are two ways to answer the question “How long is the ball in the air?” First way: Since it takes \(3\)s for the ball to reach its maximum altitude, it follows that it will take another \(3\)s to reach the ground, for a total time of \(6\)s in the air. Second way: When the ball reaches the ground, \(s=s( t) =0\). Solve for \(t\): \[ \begin{eqnarray*} s( t) &=&-4.9t^{2}+29.4t=0\\[4pt] && t (-4.9t + 29.4) =0\\[4pt] t&=&0\qquad \hbox{or}\qquad t=\frac{29.4}{4.9}=6 \end{eqnarray*} \]

The ball is at ground level at \(t=0\) and at \(t=6\), so the ball is in the air for 6 seconds.

(f) Upon impact with the ground, \(t=6s\). So the velocity is \[ v( 6) =(-9.8)(6)+29.4=-29.4 \]

Upon impact the direction of the ball is downward, and its speed is 29.4m/s.

(g) The total distance traveled by the ball is \[ s(3) +s(3) =2~s(3) =2( 44.1) =88.2{m} \]

See Figure 25 for an illustration.