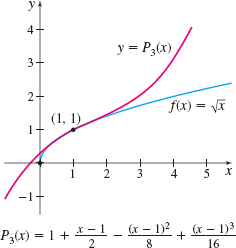
Finding a Taylor Polynomial for \(f( x)=\sqrt{x}\)

Find the Taylor Polynomial \(P_{3}( x) \) for \(f( x) =\sqrt{x}\) at \(1.\)

Solution The first three derivatives of \(f(x) =\sqrt{x}\) are \[ \begin{eqnarray*} f^\prime ( x) &=&\dfrac{1}{2\sqrt{x}}\qquad\qquad f^{\prime \prime} ( x) =\dfrac{d}{dx}\left( \dfrac{x^{-1/2}}{2}\right) =-\dfrac{1}{4x^{3/2}} \\ f^{\prime \prime \prime} ( x) &=&\dfrac{d}{dx}\left( -\dfrac{x^{-3/2}}{4}\right) =\dfrac{3}{8x^{5/2}} \end{eqnarray*} \]

Then \[ f(1) =1\qquad f^\prime (1) =\dfrac{1}{2}\qquad f^{\prime \prime} (1) =-\dfrac{1}{4}\qquad f^{\prime \prime \prime} (1) =\dfrac{3}{8} \]

The Taylor Polynomial \(P_{3}( x) \) for \(f( x) =\sqrt{x} \) at \(1\) is \[ \begin{eqnarray*} P_{3}( x) &=&f(1) +f^\prime (1) ( x-1) +\dfrac{f^{\prime \prime} (1) }{2!}( x-1) ^{2}+\dfrac{f^{\prime \prime \prime} (1) }{3!}( x-1)^{3}\\ &=&1+\dfrac{x-1}{2}-\dfrac{( x-1) ^{2}}{8}+\dfrac{( x-1) ^{3}}{16} \end{eqnarray*} \]

The graphs of the function \(f\) and the Taylor Polynomial \(P_{3}\) are shown in Figure 17. Notice how \(P_{3}( x) \approx f( x)\) for values of \(x\) near \(1\).