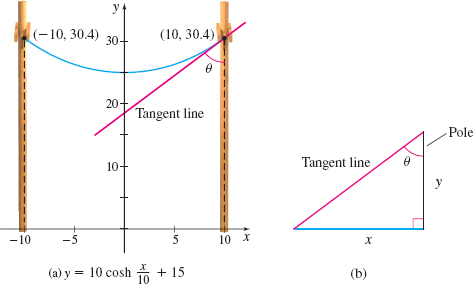
Finding the Angle Between a Catenary and Its Support
A cable is suspended between two poles of the same height that are \(20{\,{\rm{m}}}\) apart, as shown in Figure 29(a). If the poles are placed at \((-10,0) \) and \((10,0)\), the equation that models the height of the cable is \(y=10\cosh \dfrac{x}{10}+15\). Find the angle \(\theta \) at which the cable meets a pole.
The slope of the tangent line to the catenary is given by \[ y^\prime =\dfrac{d}{dx}\left( 10\cosh \dfrac{x}{10}+15\right) =10\cdot \dfrac{ 1}{10}\sinh \dfrac{x}{10}=\sinh \dfrac{x}{10} \]
At \(x=10,\) the slope \(m_{\tan }\) of the tangent line is \(m_{\tan }=\sinh \dfrac{10}{10}=\sinh 1.\)
The angle \(\theta \) at which the cable meets the pole equals the angle between the tangent line and the pole. To find \(\theta ,\) we form a right triangle using the tangent line and the pole, as shown in Figure 29(b).
From Figure 29(b), we find that the slope of the tangent line is \(m_{\tan }=\dfrac{\Delta y}{\Delta x}=\sinh 1.\) Then \(\tan \theta =\dfrac{\Delta x}{\Delta y}=\dfrac{1}{\sinh 1}.\) So, \(\theta =\tan ^{-1}\left( \dfrac{1}{\sinh 1}\right) \approx 0.7050\) radians \(\approx 404^{\circ}\).