Finding an Equation of a Tangent Line

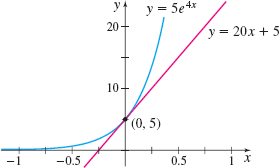
Find an equation of the tangent line to the graph of \(y=5e^{4x}\) at the point \(( 0,5) .\)

Solution The slope of the tangent line to the graph of \(y=f( x) \) at the point \(( 0,5) \) is \(f^\prime ( 0) \). \[ \begin{eqnarray*} f^\prime (x) &=& \dfrac{d}{dx}( 5e^{4x}) \underset{\underset{\color{#0066A7}{\hbox{Mulitple Rule}}}{\underset{\color{#0066A7}{\hbox{Constant}}}{\color{#0066A7}{{\uparrow}}}}}{=} 5\dfrac{d}{dx}e^{4x} \underset{\underset{\underset{\color{#0066A7}{{{\hbox{\(\tfrac{d}{dx}{e}^{u}{= e}^{u} \tfrac{du}{dx}\)}}}}}{\color{#0066A7}{{{\hbox{\(u=4x;\)}}}}}}{\color{#0066A7} {{\uparrow}}}}{=} 5e^{4x}\,{\cdot}\,\dfrac{d}{dx}(4x)=5e^{4x}\,{\cdot}\,4=20e^{4x}\\ \end{eqnarray*} \] \(m_{\tan }=\) \(f^\prime ( 0) =20e^{0}=20\). Using the point slope form of a line, we have \[ \begin{eqnarray*} y-5 &=&20( x-0)\qquad {\color{#0066A7}{y-y_{0} = m_{\tan }( { x-x}_{{ 0}})}}\\ y &=&20x+5 \end{eqnarray*} \]