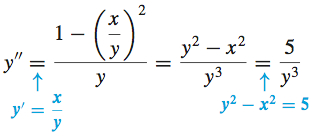Finding Higher-Order Derivatives

Use implicit differentiation to find \(y^\prime \) and \(y^{\prime\prime} \) if \(y^{2}-x^{2}=5\). Express \(y^{\prime\prime} \) in terms of \(x\) and \(y\).

Solution First, we assume there is a differentiable function \(y=f( x) \) that satisfies \(y^{2}-x^{2}=5\). Now we find \(y^\prime \).



provided \(y≠ 0\).

213

Equations (3) and (4) both involve \(y^\prime \). Either one can be used to find \(y^{\prime\prime} .\) We use (3) because it avoids differentiating a quotient. \[ \begin{eqnarray*} \dfrac{d}{dx} ( 2yy^\prime -2x) &=&\dfrac{d}{dx}0 \nonumber\\ \dfrac{d}{dx} ( yy^\prime ) -\dfrac{d}{dx}x &=&0 \nonumber\\ y\cdot \dfrac{d}{dx}y^\prime +\left( \dfrac{d}{dx}y\right) y^\prime -1 &=&0 \nonumber\\ yy^{\prime\prime} +( y^\prime ) ^{2}-1 &=&0 \nonumber\\ y^{\prime\prime} &=&\dfrac{1-( y^\prime ) ^{2}}{y}\tag{5} \end{eqnarray*} \] provided \(y≠ 0\). To express \(y^{\prime\prime} \) in terms of \(x\) and \(y,\) we use (4) and substitute for \(y^\prime \) in (5).