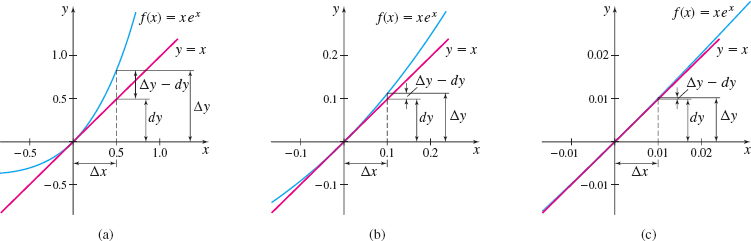
Finding and Interpreting Differentials Geometrically
For the function \(f(x) =xe^{x}\):
- Find the differential \(dy\).
- Compare \(dy\) to \(\Delta y\) when \(x=0\) and \(\Delta x=0.5.\)
- Compare \(dy\) to \(\Delta y\) when \(x=0\) and \(\Delta x=0.1\).
- Compare \(dy\) to \(\Delta y\) when \(x=0\) and \(\Delta x=0.01\).
- Discuss the results.
(b) See Figure 9(a). When \(x=0\) and \(\Delta x=dx=0.5\), then \[ \ dy=(x+1) e^{x}dx=(0+1) e^{0}(0.5) =0.5 \]
232
The tangent line rises by \(0.5\) as \(x\) changes from \(0\) to \(0.5\). The corresponding change in the height of the graph \(f\) is \[ \begin{eqnarray*} \Delta y=f( x+\Delta x) -f( x) &=&f(0.5) -f( 0) =0.5e^{0.5}-0\approx 0.824\\ \vert \Delta y-dy\vert &\approx& \vert 0.824-0.5\vert =0.324 \end{eqnarray*} \]
The graph of the tangent line is approximately \(0.324\) below the graph of \(f\) at \(x\,{=}\,0.5\).
(c) See Figure 9(b). When \(x=0\) and \(\Delta x=dx=0.1\), then \[ dy=(0+1) e^{0}(0.1) =0.1 \]
The tangent line rises by \(0.1\) as \(x\) changes from \(0\) to \(0.1.\) The corresponding change in the height of the graph \(f\) is \[ \begin{eqnarray*} \Delta y=f( x+\Delta x) -f( x) &=&f(0.1) -f( 0) =0.1e^{0.1}-0\approx 0.111\\ \vert \Delta y-dy\vert &\approx& \left\vert 0.111-0.1\right\vert =0.011 \end{eqnarray*} \]
The graph of the tangent line is approximately \(0.011\) below the graph of \(f\) at \(x=0.1\).
(d) See Figure 9(c). When \(x=0\) and \(\Delta x=dx=0.01\), then \[ dy=(0+1) e^{0}( 0.01) =0.01 \]
The tangent line rises by \(0.01\) as \(x\) changes from \(0\) to \(0.01.\) The corresponding change in the height of the graph of \(f\) is \[ \begin{eqnarray*} \Delta y=f( x+\Delta x) -f( x) &=&f( 0.01) -f( 0) =0.01e^{0.01}-0\approx 0.0101\\ \vert \Delta y-dy\vert &\approx& \vert 0.0101-0.01\vert =0.0001 \end{eqnarray*} \]
The graph of the tangent line is approximately \(0.0001\) below the graph of \(f\) at \(x=0.01\).
(e) The closer \(\Delta x\) is to \(0\), the closer \(dy\) is to \(\Delta y.\) So, we conclude that the closer \(\Delta x\) is to \(0\), the less the tangent line departs from the graph of the function. That is, we can use the tangent line to \(f\) at a point \(P\) as a linear approximation to \(f\) near \(P\).