Using Newton’s Method to Approximate a Real Zero of a Function

Use Newton’s Method to find a fourth approximation to the positive real zero of the function \(f( x) =x^{3}+x^{2}-x-2\).

Solution Since \(f(1) =-1\) and \(f(2) =8,\) we know from the Intermediate Value Theorem that \(f\) has a zero in the interval \((1, 2) \). Also, since \(f\) is a polynomial function, both \(f\) and \(f^\prime \) are differentiable functions. Now \[ f(x) =x^{3}+x^{2}-x-2 \qquad \hbox{and}\qquad f^\prime ( x) =3x^{2}+2x-1 \]

236

We choose \(c_{1}=1.5\) as the first approximation and use Newton’s Method. The second approximation to the zero is \[ c_{2}=c_{1}-\dfrac{f( c_{1}) }{f^\prime ( c_{1}) }=1.5-\dfrac{f(1.5) }{f^\prime (1.5) }=1.5-\dfrac{2.125}{ 8.75}\approx 1.2571429 \]

Use Newton’s Method again, with \(c_{2}=1.2571429\). Then \(f(1.2571429) \approx 0.3100644\) and \(f^\prime (1.2571429)\approx 6.2555106\). The third approximation to the zero is \[ c_{3}=c_{2}-\dfrac{f( c_{2}) }{f^\prime ( c_{2}) }=1.2571429-\dfrac{0.3100641}{6.2555102}\approx 1.2075763 \]

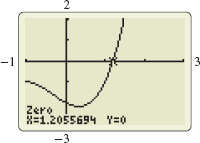
The fourth approximation to the zero is \[ c_{4}=c_{3}-\dfrac{f( c_{3}) }{f^\prime ( c_{3}) } =1.2075763-\dfrac{0.0116012}{5.7898745}\approx 1.2055726 \]