Using Technology with Newton’s Method

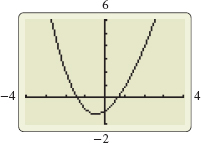
The graph of the function \(f( x) =\sin x+x^{2}-1\) is shown in Figure 14.

1. Use the Intermediate Value Theorem to confirm that \(f\) has a zero in the interval \((0,1) \).
2. Use graphing technology with Newton’s Method and a first approximation of \(c_{1}= 0.5\) to find a fourth approximation to the zero.

Solution (a) The function \(f( x) =\sin x+x^{2}-1\) is continuous on its domain, all real numbers, so it is continuous on the closed interval \([0,1] .\) Since \(f( 0) =-1\) and \(f(1) =\sin 1\approx 0.841\) have opposite signs, the Intermediate Value Theorem guarantees that \(f\) has a zero in the interval \((0,1) .\)

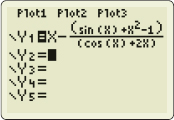
(b) We begin by finding \(f^\prime ( x) =\cos x+2x.\) To use Newton’s Method with a graphing utility, we enter \[ x-\dfrac{\sin x+x^{2}-1}{\cos x+2x} \qquad {\color{#0066A7}{x-\dfrac{{ f}({x}) }{{ f^\prime }({x})}}} \]

into the \(Y= \hbox{editor}\), as shown in Figure 15. We create a table by entering the initial value \(0.5\) in the \(X\) column. The graphing utility computes \[ 0.5-\dfrac{\sin 0.5+0.5^{2}-1}{\cos 0.5+2(0.5) }=0.64410789 \]

and displays \(0.64411\) in column \(Y_{1}\) next to \(0.5.\) The value \(Y_{1}\) is the second approximation \(c_{2}\) that we use in the next iteration. That is, we enter \(0.64410789\) in the \(X\) column of the next row, and the new entry in column \(Y_{1}\) is the third approximation \(c_{3}.\) We repeat the process until we obtain the desired approximation. The fourth approximation to the zero of \(f\) is \(0.63673\), as shown in Figure 16.