Using Calculus to Graph a Rational Function
Graph \(f(x)=\dfrac{6x^{2}-6}{x^{3}}\).
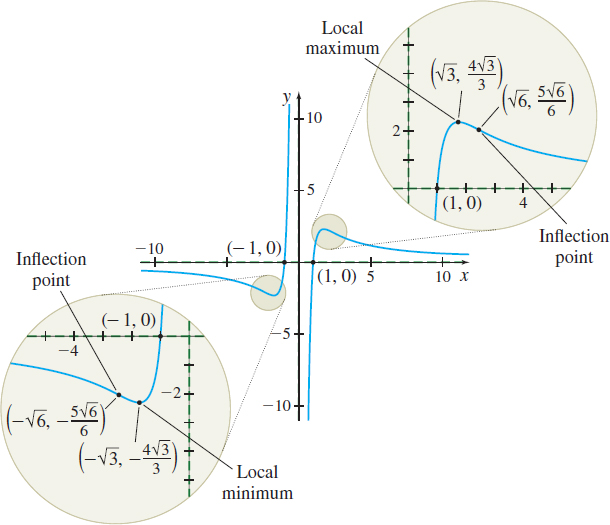
Step 1 \(f\) is a rational function; the domain of \(f\) is \(\{ x|x\neq 0\} \). The \(x\)-intercepts are \(-1\) and \(1\). There is no \(y\)-intercept. We plot the intercepts \((-1,0)\) and \((1,0) .\)
Step 2 The degree of the numerator is less than the degree of the denominator, so \(f\) has a horizontal asymptote. We find the horizontal asymptotes by finding the limits at infinity. Using L’Hôpital’s Rule, we get \[ \lim\limits_{x\rightarrow \infty }\frac{6x^{2}-6}{x^{3}}=\lim\limits_{x \rightarrow \infty }\dfrac{12x}{3x^{2}}=\lim\limits_{x\rightarrow \infty } \frac{12}{6x}=0 \]
The line \(y=0\) is a horizontal asymptote as \(x\rightarrow -\infty\) and as \(x\rightarrow \infty \).
We identify vertical asymptotes by checking for infinite limits. [\(\lim\limits_{x\rightarrow 0}f(x) \) is the only one to check–do you see why?] \[ \lim\limits_{x\rightarrow 0^{-}}{\frac{6x^{2}-6}{x^{3}}}=\infty \qquad \lim\limits_{x\rightarrow 0^{+}}{\frac{6x^{2}-6}{x^{3}}} =-\infty \]
The line \(x=0\) is a vertical asymptote. We draw the asymptotes on the graph.
310
Step 3 \[ \begin{array}{l} f'(x) &=& \frac{d}{{dx}}\left( {\frac{{6x^2 - 6}}{{x^3 }}} \right) = \frac{{12x(x^3 ) - (6x^2 - 6)(3x^2 )}}{{x^6 }} \\ &=& \frac{{6x^2 (3 - x^2 )}}{{x^6 }} = \frac{{6(3 - x^2 )}}{{x^4 }} \\ f''(x) &=& \frac{d}{{dx}}\left[ {\frac{{6(3 - x^2 )}}{{x^4 }}} \right] = 6 \cdot \frac{{( - 2x)x^4 - (3 - x^2 )(4x^3 )}}{{x^8 }} \\ &=& \frac{{12x^3 (x^2 - 6)}}{{x^8 }} = \frac{{12(x^2 - 6)}}{{x^5 }} \\ \end{array} \]
Critical numbers occur where \(f^\prime (x) =0\) or where \(f^\prime (x)\) does not exist. Since \(f^\prime (x) =0\) when \(x=\pm \sqrt{3}\), there are two critical numbers, \(\sqrt{3}\) and \(-\sqrt{3}\). (The derivative does not exist at \(0\), but, since \(0\) is not in the domain of \(f\), it is not a critical number.)
Step 4 To apply the Increasing/Decreasing Function Test, we use the numbers \(-\sqrt{3},\) \(0,\) and \(\sqrt{3}\) to form four intervals.
| Interval | Sign of f\(^\prime\) | Conclusion |
|---|---|---|
| \(( -\infty ,-\sqrt{3})\) | negative | \(f\) is decreasing on \(( -\infty ,-\sqrt{3})\) |
| \(( -\sqrt{3},0)\) | positive | \(f\) is increasing on \(( - \sqrt{3},0)\) |
| \((0,\sqrt{3})\) | positive | \(f\) is increasing on \(( 0, \sqrt{3})\) |
| \(( \sqrt{3},\infty )\) | negative | \(f\) is decreasing on \(( \sqrt{3},\infty )\) |
Step 5 We use the First Derivative Test. From the table in Step 4, we conclude
- \(f( -\sqrt{3}) =\) \(-\dfrac{4}{\sqrt{3 }}\approx -2.31\) is a local minimum value.
- \(f(\sqrt{3}) =\) \(\dfrac{4}{\sqrt{3}}\approx 2.31\) is a local maximum value
Plot the local extreme points.
Step 6 We use the Test for Concavity. \(f^{\prime \prime} (x) =\dfrac{12( x^{2}-6) }{x^{5}}=0\) when \(x=\pm \sqrt{6}\). Now use the numbers \(-\sqrt{6},\) \(0,\) and \(\sqrt{6}\) to form four intervals.
| Interval | Sign of f\(^{\prime \prime}\) | Conclusion |
|---|---|---|
| \(( -\infty ,-\sqrt{6})\) | negative | \(f\) is concave down on \(( -\infty ,-\sqrt{6})\) |
| \((-\sqrt{6},0)\) | positive | \(f\) is concave up on \(( -\sqrt{6},0)\) |
| \( 0,\sqrt{6}\) | negative | \(f\) is concave down on \(( 0,\sqrt{6})\) |
| \(( \sqrt{6},\infty )\) | positive | \(f\) is concave up on \(( \sqrt{6},\infty )\) |
The concavity of the function \(f\) changes at \(-\sqrt{6},\) \(0,\) and \(\sqrt{6}\). So, theeak points \(\left( -\sqrt{6},-\dfrac{5\sqrt{6}}{6}\right)\) and \(\left( \sqrt{6},\dfrac{5\sqrt{6}}{6}\right)\) are inflection points. Since \(0\) is not in the domain of \(f,\) there is no inflection point at \(0.\) We plot the inflectioneak points.
Step 7 We now use the information about where the function increases/decreases and the concavity to complete the graph. See Figure 47. Notice the apparent symmetry of the graph with respect to the origin. We can verify this symmetry by showing \(f( -x) =-f(x)\) and concluding that \(f\) is an odd function.
311
