Using Calculus to Graph a Rational Function
Graph \(f(x) =\dfrac{x^{2}-2x+6}{x-3}\).
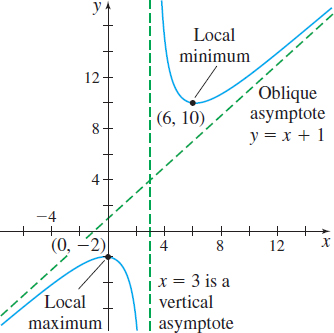
Step 1 \(f\) is a rational function; the domain of \(f\) is \(\{ x|x\neq 3\}\). There are no \(x\)-intercepts, since \( x^{2}-2x+6=0\) has no real solutions. (Its discriminant is negative.) The \(y\) -intercept is \(f( 0) =-2\). Plot the intercept \(( 0,-2).\)
Step 2 We identify any vertical asymptotes by checking for infinite limits (\(3\) is the only number to check). Since \(\lim\limits_{x\rightarrow 3^{-}}\left( \dfrac{x^{2}-2x+6}{x-3}\right) =-\infty \) and \(\lim\limits_{x\rightarrow 3^{+}}\left( \dfrac{x^{2}-2x+6}{x-3 }\right) =\infty \), the line \(x=3\) is a vertical asymptote.
312
The degree of the numerator of \(f\) is 1 more than the degree of the denominator, so \(f\) will have an oblique asymptote. We divide \(x^{2}-2x+6\) by \( x-3\) to find the line \(y=mx+b\). \[ f(x) =\frac{x^{2}-2x+6}{x-3}=x+1+\frac{9}{x-3} \]
Since \( \lim\limits_{x\rightarrow \infty }[ f(x) -( x+1) ] =\lim\limits_{x\rightarrow \infty }\dfrac{9}{x-3}=0,\) then \(y=x+1\) is an oblique asymptote of the graph of \(f\). Draw the asymptotes on the graph.
Step 3\[ \begin{eqnarray*} f^\prime (x) &=&\dfrac{d}{\textit{dx}}\left( \dfrac{x^{2}-2x+6}{x-3}\right) =\dfrac{( 2x-2) (x-3) -( x^{2}-2x+6) ( 1) }{(x-3) ^{2}}\\ &=&\dfrac{ x^{2}-6x}{(x-3)^{2}}=\dfrac{x( x-6) }{(x-3) ^{2}}\\ f^{\prime \prime} (x) &=&\dfrac{d}{\textit{dx}}\left[ \dfrac{x^{2}-6x}{ (x-3) ^{2}}\right] =\dfrac{( 2x-6) (x-3) ^{2}-( x^{2}-6x) [ 2(x-3) ] }{(x-3) ^{4}} \\ &=&(x-3) \dfrac{( 2x^{2}-12x+18) -( 2x^{2}-12x) }{(x-3) ^{4}}=\dfrac{18}{(x-3) ^{3} } \end{eqnarray*} \]
\(f^\prime (x) =0\) at \(x=0\) and at \(x=6\). So, \(0\) and \(6\) are critical numbers. The tangent lines are horizontal at \(0\) and at \(6.\) Since \(3\) is not in the domain of \(f\), \(3\) is not a critical number.
Step 4 To apply the Increasing/Decreasing Function Test, we use the numbers \(0,\) \(3,\) and \(6\) to form four intervals.
| Interval | Sign of f\(^\prime(x)\) | Conclusion |
|---|---|---|
| \((-\infty ,0)\) | positive | \(f\) is increasing on \((-\infty ,0)\) |
| \((0,3)\) | negative | \(f\) is decreasing on \((0,3)\) |
| \(\left( 3,6\right)\) | negative | \(f\) is decreasing on \(\left( 3,6\right)\) |
| \(\left( 6,\infty \right)\) | positive | \(f\) is increasing on \(\left(6,\infty \right) \) |
Step 5 Using the First Derivative Test, we find that \(f( 0) =-2\) is a local maximum value and \(f( 6) =10\) is a local minimum value. Plot the points \(\left( 0,-2\right)\) and \(\left( 6,10\right)\).
Step 6 \(f^{\prime \prime} (x) =\dfrac{18}{(x-3) ^{3}}\). If \(x<3\), \(f^{\prime \prime} (x) <0\), and if \(x>3\) , \(f^{\prime \prime} (x) >0\). From the Test for Concavity, we conclude \(f\) is concave down on the interval \(\left( -\infty ,3\right)\) and \(f\) is concave up on the interval \((3,\infty) \). The concavity changes at \(3\), but \(3\) is not in the domain of \(f\). So, the graph of \(f\) has no inflection point.
Step 7 We use the information to complete the graph of the function. See Figure 48.
