Using Calculus to Graph a Trigonometric Function
Graph \(f(x)=\sin x-\cos ^{2}x,\) \(0\leq x\leq 2\pi\) .
Step 1 The domain of \(f\) is \(\{ x|0\leq x\leq 2\pi \} \). Since \(f( 0) =\sin 0-\cos ^{2}0=-1\), the \(y\)-intercept is \(-1\). The \(x\)-intercepts satisfy the equation \[ \sin x-\cos ^{2}x=\sin x-( 1-\!\sin ^{2}x) =\sin ^{2}x+\sin x-1=0 \]
This trigonometric equation is quadratic in form, so we use the quadratic formula. \[ \sin x=\dfrac{-1\pm \sqrt{1-4( 1) (-1) }}{2}=\dfrac{ -1\pm \sqrt{5}}{2} \]
Trigonometric equations are discussed in Section P. 7, pp. 61-63.
Since \(\dfrac{-1-\sqrt{5}}{2}<-1\) and \(-1\leq \sin x\leq 1\), the \(x\) -intercepts occur at \(x=\sin ^{-1}\left( \dfrac{-1+\sqrt{5}}{2}\right) \approx 0.67\) and at \(x=\pi -\sin ^{-1}\left( \dfrac{-1+\sqrt{5}}{2}\right) \approx 2.48.\) Plot the intercepts.
Step 2 The function \(f\) has no asymptotes.
Step 3 \[ \begin{array}{@{}rcl} f' (x)&=&\dfrac{d}{\textit{dx}}( \sin x-\cos ^{2} x) =\cos x+2\, \cos\, x\, \sin x=\cos x(1+2\sin x)\\ f'' (x)& =&\dfrac{d}{\textit{dx}}[ {\cos x(1+2\sin x)}] =2\, \cos ^{2}x-\!\sin x(1+2\sin x)\\ &=&2\cos ^{2}x-\!\sin x-2\sin ^{2}x=-4\sin ^{2}x-\!\sin x+2 \end{array} \]
The critical numbers occur where \(f^\prime (x) =0\). That is, where \[ \cos x=0 \qquad\hbox{or}\qquad 1+2\sin x=0 \]
315
In the interval \([0,2\pi ] \): \(\cos x=0\) if \(x=\dfrac{\pi }{2}\) or if \(x=\dfrac{3\pi }{2}\); and \(1+2\sin x=0\) when \(\sin x=-\dfrac{1}{2}\), that is, when \(x=\dfrac{7\pi }{6}\) or \(x=\dfrac{11\pi }{6}\). So, the critical numbers are \(\dfrac{\pi }{2}\), \(\dfrac{7\pi }{6}\), \(\dfrac{3\pi }{2}\), and \(\dfrac{11\pi }{6}\). At each of these numbers, the tangent lines are horizontal.
Step 4 To apply the Increasing/Decreasing Function Test, we use the numbers \(0,\) \(\dfrac{\pi }{2}\), \(\dfrac{7\pi }{6}\), \(\dfrac{3\pi }{2}\), \( \dfrac{11\pi }{6},\) and \(2\pi\) to form five intervals.
| Interval | Sign of fs\(^\prime\) | Conclusion |
|---|---|---|
| \(\left( 0,\dfrac{\pi }{2}\right)\) | positive | \(f\) is increasing on \(\left( 0,\dfrac{\pi }{2}\right)\) |
| \(\left( \dfrac{\pi }{2},\dfrac{7\pi }{6}\right)\) | negative | \(f\) is decreasing on \(\left( \dfrac{\pi }{2},\dfrac{7\pi}{6}\right)\) |
| \(\left(\dfrac{7\pi}{6},\dfrac{3\pi}{2}\right)\) | positive | \(f\) is increasing on \(\left( \dfrac{7\pi }{6},\dfrac{3\pi}{2}\right)\) |
| \(\left( \dfrac{3\pi }{2},\dfrac{11\pi }{6}\right)\) | negative | \(f\) is decreasing on \(\left( \dfrac{3\pi }{2},\dfrac{11\pi }{6}\right)\) |
| \(\left( \dfrac{11\pi }{6},2\pi \right)\) | positive | \(f\) is increasing on \(\left( \dfrac{11\pi }{6},2\pi \right)\) |
Step 5 By the First Derivative Test, \(f\left( \dfrac{\pi }{2} \right) =1\) and \(f\left( \dfrac{3\pi }{2}\right) =-1\) are local maximum values, and \(f\left(\dfrac{7\pi}{6}\right) =-\dfrac{5}{4}\) and \(f\left(\dfrac{11\pi}{6}\right) =-\dfrac{5}{4}\) are local minimum values. Plot these points.
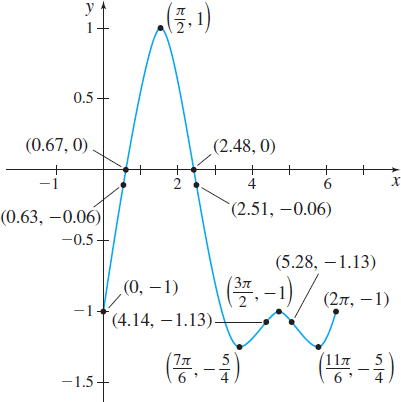
Step 6 We apply the Test for Concavity. To solve \(f^{\prime \prime} (x) >0\) and \(f^{\prime \prime} (x) <0\), we first solve the equation \(f^{\prime \prime} (x) =-4\sin ^{2}x-\!\sin x+2=0,\) or equivalently, \[ \begin{eqnarray*} 4\sin ^{2}x+\sin x-2 &=&0 \qquad 0\leq x\leq 2\pi \\[3pt] \sin x &=&\dfrac{-1\pm \sqrt{1+32}}{8} \\[3pt] \sin x &\approx &0.593\qquad \hbox{or}\qquad \sin x\approx -0.843 \\ x &\approx &0.63 \qquad x\approx 2.51 \qquad x\approx 4.14 \qquad x\approx 5.28 \end{eqnarray*} \]
We use these numbers to form five subintervals of \([0,2\pi ]\).
| Interval | Sign of f\(^{\prime \prime}\) | Conclusion |
|---|---|---|
| \((0,0.63)\) | positive | \(f\) is concave up on the interval \(( 0,0.63)\) |
| \(( 0.63,2.51)\) | negative | \(f\) is concave down on the interval \(( 0.63,2.51)\) |
| \(( 2.51,4.14)\) | positive | \(f\) is concave up on the interval \(( 2.51,4.14)\) |
| \(( 4.14,5.28)\) | negative | \(f\) is concave down on the interval \(( 4.14,5.28)\) |
| \(( 5.28,2\pi )\) | positive | \(f\) is concave up on the interval \(( 5.28,2\pi )\) |
The inflection points are \(( 0.63,-0.06) \), \((2.51,-0.06) \), \(( 4.14,-1.13) \), and \(( 5.28,-1.13) .\) Plot the inflection points.
The function \(f\) in Example 6 is periodic with period \(2\pi\). To graph this function over its unrestricted domain, the set of real numbers, repeat the graph in Figure 51 over intervals of length \(2\pi\).
Step 7 The graph of \(f\) is given in Figure 51.