Figure

EXAMPLE 7Using Calculus to Graph a Function

Graph $f(x)=e^{x}( x^{2}-3)$ .

Solution

Step 1 The domain of $f$ is all real numbers. Since $f( 0) =-3$ , the $y$ -intercept is $-3$ . The $x$ -intercepts occur where $\begin{eqnarray*} f(x) &=&e^{x}( x^{2}-3) =0 \\[3pt] x &=&\sqrt{3}\qquad\hbox{or}\qquad x=-\sqrt{3} \end{eqnarray*}$

Plot the intercepts.

Step 2 Since the domain of $f$ is all real numbers, there are no vertical asymptotes. To determine if there is a horizontal asymptote, we find the limits at infinity. $\lim\limits_{x\rightarrow -\infty }f(x) =\lim\limits_{x\rightarrow -\infty } [ e^{x} ( x^{2}-3 ) ]$

Since $e^{x} ( x^{2}-3 )$ is an indeterminate form at $-\infty$ of the type $0\cdot \infty$ , we write $e^{x} ( x^{2}-3 ) =\dfrac{x^{2}-3}{e^{-x}}$ and use L’Hôpital’s Rule.

The line $y=0$ is a horizontal asymptote as $x\rightarrow -\infty$ .

Since $\lim\limits_{x\rightarrow \infty }[ e^{x}( x^{2}-3) ] =\infty ,$ there is no horizontal asymptote as $x\rightarrow \infty .$ Draw the asymptote on the graph.

Step 3 $\begin{array}{@{}rcl} f^\prime (x) &=&\dfrac{d}{\textit{dx}}[e^{x}( x^{2}-3) ] =e^{x}(2x) +e^{x}(x^{2}-3) =e^{x}( x^{2}+2x-3)\\[8pt] &=&e^{x}( x+3) ( x-1)\\[11pt] f^{\prime \prime} (x) &=&\dfrac{d}{\textit{dx}}[e^{x}( x^{2}+2x-3) ] =e^{x}( 2x+2) +e^{x}(x^{2}+2x-3)\\[8pt] &=&e^{x}( x^{2}+4x-1) \end{array}$

Solving $f^\prime (x) =0,$ we find that the critical numbers are $-3$ and $1$ .

Step 4 To apply the Increasing/Decreasing Function Test, we use the critical numbers $-3$ and $1$ to form three intervals.

Interval	Sign of f $^\prime$	Conclusion
$( -\infty ,-3)$	positive	$f$ is increasing on the interval $( -\infty ,-3)$
$(-3,1)$	negative	$f$ is decreasing on the interval $( -3,1)$
$(1,\infty )$	positive	$f$ is increasing on the interval $(1,\infty )$

Step 5 We use the First Derivative Test to identify the local extrema. From the table in Step 4, there is a local maximum at $-3$ and a local minimum at $1.$ Then $f(-3) =6e^{-3}\approx 0.30$ is a local maximum value and $f(1) =-2e\approx -5.44$ is a local minimum value. Plot the local extrema.

317

Figure 52

$f(x)=e^x(x^2-3)$

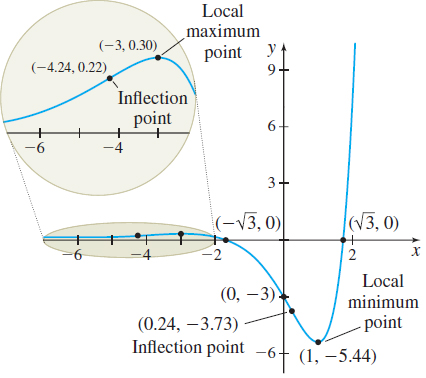
Step 6 To determine the concavity of $f,$ first we solve $f^{\prime \prime} (x) =0$ . We find $x=-2\pm \sqrt{5}$ . Now we use the numbers $-2-\sqrt{5}\approx -4.24$ and $-2+\sqrt{5}\approx 0.24$ to form three intervals and apply the Test for Concavity.

Interval	Sign of ${f''}$	Conclusion
$( -\infty ,-2-\sqrt{5})$	positive	$f$ is concave up on the interval $(-\infty ,-2 - \sqrt{5})$
$(-2-\sqrt{5},-2+\sqrt{5})$	negative	$f$ is concave down on the interval $( -2 -\sqrt{5}, -2+\sqrt{5})$
$(-2+\sqrt{5},\infty)$	positive	$f$ is concave up on the interval $( -2+\sqrt{5},\infty )$

The inflection points are $( -4.24,0.22)$ and $( 0.24,-3.73) .$ Plot the inflection points.

Step 7 The graph of $f$ is given in Figure 52.