Maximizing a Volume

From each corner of a square piece of sheet metal \(18\) \({\rm{cm}}\) on a side, we remove a small square and turn up the edges to form an open box. What are the dimensions of the box with the largest volume?

Solution

Step 1 The quantity to be maximized is the volume of the box; we denote it by \(V\). We denote the length of each side of the small squares by \(x\) and the length of each side after the small squares are removed by \(y,\) as shown in Figure 54. Both \(x\) and \(y\) are in centimeters.

320

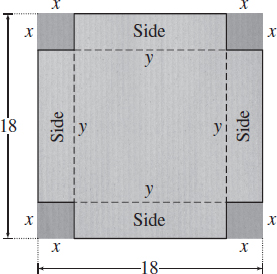
Step 2 Then \(y=( 18-2x) \ {\rm{cm}}\). The height of the box is \(x \ {\rm{cm}}\), and the area of the base of the box is \(y^{2}\ {\rm{cm}}^{2}\). So, the volume of the box is \(V=x{y^{2}}\ {\rm{cm}}^{3}.\)

Step 3 To express \(V\) as a function of one variable, we substitute \( y=18-2x\) into the formula for \(V\). Then the function to be maximized is \[ V=V(x) =x({18-2x})^{2} \]

Since both \(x\geq 0\) and \(18-2x\geq 0,\) we find \(x\leq 9\), meaning the domain of \(V\) is the closed interval \([ 0,9] .\) (All other numbers make no physical sense—do you see why?)

Step 4 To find the value of \(x\) that maximizes \(V\), we differentiate \(V\) and find the critical numbers: \[ {{V^\prime }(x)}=2x({18-2x})({-2})+({18-2x})^{2}=({18-2x})({18-6x}) \]

Now, we solve \(V^\prime (x)=0\) for \(x\). The solutions are \[ x=9\qquad \hbox{or}\qquad x=3 \]

The only critical number in the open interval \((0,9)\) is \(3\). We evaluate \(V\) at \(3\) and at the endpoints \(0\) and \(9\). \[ V(0)=0\qquad V(3)=3(18-6)^{2}=432 \qquad V(9)=0 \]

The maximum volume is \(432\ {\rm{cm}}^{3}\). The box with the maximum volume has a height of \(3\ {\rm{cm}}\). Since \(y=18-2(3) =12\ {\rm{cm}}\), the base of the box measures \(12\ {\rm{cm}}\) by \(12\ {\rm{cm}}\).