Maximizing an Area

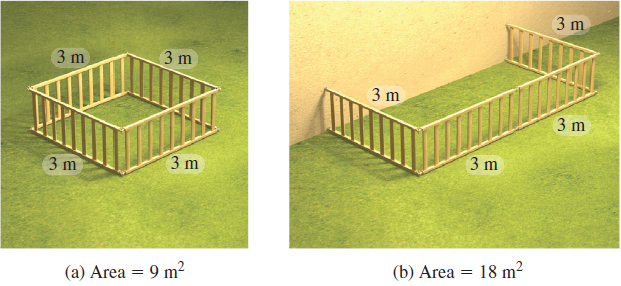
A manufacturer makes a flexible square play yard (Figure 55a), that can be opened at one corner and attached at right angles to a wall or the side of a house, as shown in Figure 55(b). If each side is \(3\ {\rm{m}}\) in length, the open configuration doubles the available area from \(9\ {\rm{m}}^{2}\) to \(18\ {\rm{m}} ^{2}\). Is there a configuration that will more than double the play area?

Solution

Step 1 We want to maximize the play area \(A.\)

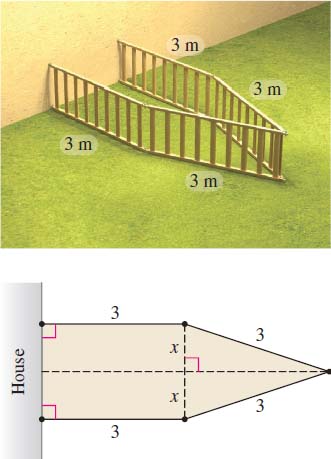
Step 2 Since the play yard must be attached at right angles to the wall, the possible configurations depend on the amount of wall used as a fifth side, as shown in Figure 56. We use \(x\) to represent half the length (in meters) of the wall used as the fifth side.

321

Step 3 We partition the play area into two sections: a rectangle with area \(3(2x) =6x\) and a triangle with base \(2x\) and altitude \( \sqrt{3^{2}-x^{2}}=\sqrt{9-x^{2}}\). The play area \(A\) is the sum of the areas of the two sections. The area to be maximized is \[ A=A(x)=6x+\dfrac{1}{2}( 2x)\sqrt{9-x^{2}} =6x+x\sqrt{9-x^{2}} \]

The domain of \(A\) is the closed interval \([ 0,3].\)

Step 4 To find the maximum area of the play yard, we find the critical numbers of \(A\). \[ \begin{eqnarray*} {A}' (x)&=&6+x\left[ \dfrac{1}{2}( -2x) ( 9-x^{2}) ^{-1/2}\right] +\sqrt{9-x^{2}}\\[5pt] &=&6-\dfrac{x^{2}}{\sqrt{9-x^{2}}}+\sqrt{9-x^{2}} =\frac{6\sqrt{9-x^{2}}-2x^{2}+9}{\sqrt{9-x^{2}}} \end{eqnarray*} \]

Critical numbers occur when \(A^\prime (x) =0\) or where \(A^\prime (x)\) does not exist. \(A^\prime\) does not exist at \(3\), and \(A^\prime (x) =0\) at \[ \begin{eqnarray*} 6\sqrt{9-x^{2}}-2x^{2}+9 &=&0 \\[3pt] \sqrt{9-x^{2}} &=&\dfrac{2x^{2}-9}{6} \\[3pt] 9-x^{2} &=&\left( \dfrac{2x^{2}-9}{6}\right) ^{\!\!2}=\dfrac{4x^{4}-36x^{2}+81}{ 36} \\[3pt] 324-36x^{2} &=&4x^{4}-36x^{2}+81 \\[3pt] 324 &=&4x^{4}+81 \\[3pt] x^{4} &=&\dfrac{324-81}{4}=\dfrac{243}{4} \\[3pt] x &=&\sqrt[{4}]{{\frac{243}{4}}}\approx 2.792 \end{eqnarray*} \]

The only critical number in the open interval \((0,3)\) is \(\sqrt[{ 4}]{{ \dfrac{243}{4}}}\approx 2.792\).

Now we evaluate \(A(x)\) at the endpoints \(0\) and \(3\) and at the critical number \( x\approx 2.792\). \[ A(0)=0\qquad A(3)=18\qquad A({2.792})\approx 19.817 \]

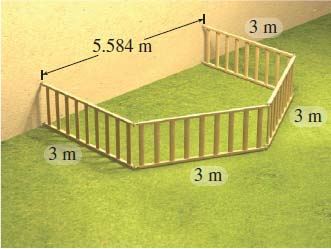
Using a wall of length \(2x\approx 2( 2.792) =5.584\ {\rm{m}}\) will maximize the area; the configuration shown in Figure 57 increases the play area by about \(10\%\) (from \(18\) to \(19.817\ {\rm{m}}^{2}\)).