Maximizing Area

A rectangle is inscribed in a semicircle of radius \(2\). Find the dimensions of the rectangle that has the maximum area.

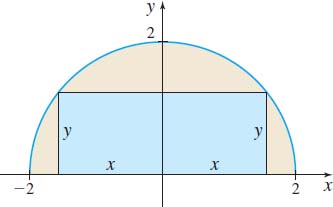
Solution We present two methods of solution: The first uses analytic geometry, the second uses trigonometry. To begin, we place the semicircle with its diameter along the \(x\)-axis and center at the origin. Then we inscribe a rectangle in the semicircle, as shown in Figure 59. The length of the inscribed rectangle is \(2x\) and its height is \(y.\)

323

Analytic Geometry Method The area \(A\) of the inscribed rectangle is \(A=2xy\) and the equation of the semicircle is \(x^{2}+y^{2}=4\), \(y\geq 0.\) We solve for \(y\) in \(x^{2}+y^{2}=4\) and obtain \(y=\sqrt{4-x^{2}}\). Now we substitute this expression for \(y\) in the area formula for the rectangle to express \(A\) as a function of \(x\) alone. \[ \begin{eqnarray*} A&=&A(x)= 2x\sqrt{4-x^{2}}\qquad 0\leq x\leq 2\\[-6.4pt] &&\hspace{-1.8pc}\color{#0066A7}{\underset{\hbox{\(A=2xy; y=\sqrt{4-x^{2}}\)}}{\uparrow}} \end{eqnarray*} \]

Then \[ \begin{eqnarray*} {A}' (x) &=&2\left[ x\left( {{\dfrac{1}{2}}}\right) \ (4-x^{2}) ^{-1/2}(-2x)+\sqrt{4-x^{2}}\right] =2\left[ \dfrac{-x^{2}}{ \sqrt{4-x^{2}}}+\sqrt{4-x^{2}}\right]\\[3pt] &=&2\left[ \frac{-x^{2}+( {4-x^{2}}) }{\sqrt{4-x^{2}}}\right] =2\left[ \frac{-2({x^{2}-2})}{\sqrt{4-x^{2}}}\right] =-\frac{4({x^{2}-2})}{\sqrt{4-x^{2}}} \end{eqnarray*} \]

The only critical number in the open interval \((0,2)\) is \(\sqrt{2}\), where \( A^\prime ( \sqrt{2}) =0.\) [\(-\sqrt{2}\) and \(-2\) are not in the domain of \(A\), and \(2\) is not in the open interval \(( 0,2)\).] The values of \(A\) at the endpoints \(0\) and \(2\) and at the critical number \(\sqrt{2}\) are \[ A(0)=0\qquad A(\sqrt{2})=4\qquad A(2)=0 \]

The maximum area of the inscribed rectangle is \(4\), and it corresponds to the rectangle whose length is \(2x=2\sqrt{2}\) and whose height is \(y=\sqrt{2}\).

Trigonometric Method Using Figure 59, we draw the radius \(r=2\) from \(O\) to the vertex of the rectangle and place the angle \(\theta\) in the standard position, as shown in Figure 60. Then \(x=2\cos \theta\) and \(y=2\sin \theta ,\) \(0\leq \theta \leq \dfrac{\pi }{2}\). The area \(A\) of the rectangle is \[ \begin{eqnarray*} A&=&2xy=2(2\, \cos \theta )(2\, \sin\, \theta )=8\, \cos \theta\, \sin\, \theta \underset{\underset{{\color{#0066A7}{\hbox{\(\sin (2\theta) =2\, \sin\, \theta \cos \theta\)}}}}{\color{#0066A7}{\uparrow}}}{=} 4\sin ( 2\, \theta )\\[-6.3pt] \end{eqnarray*} \]

Since the area \(A\) is a differentiable function of \(\theta\), we obtain the critical numbers by finding \(A^\prime (\theta )\) and solving the equation \(A^\prime (\theta ) =0\). \[ \begin{eqnarray*} A^\prime (\theta ) &=&8\, \cos ( 2\theta ) =0 \\[1pt] \cos ( 2\theta ) &=&0 \\[1pt] 2\theta &=&\cos ^{-1}0=\dfrac{\pi }{2} \\[3pt] \theta &=&\dfrac{\pi }{4} \end{eqnarray*} \]

We now find \(A^{\prime \prime} (\theta )\) and use the Second Derivative Test. \[ \begin{eqnarray*} {A}'' (\theta )&=&-16\, \sin ( 2\theta ) \\[3pt] {A}'' \left( {\dfrac{\pi }{4}}\right) &=&-16\, \sin \left( 2\cdot \dfrac{\pi }{4}\right) =-16\, \sin \dfrac{\pi }{2}=-16<0 \end{eqnarray*} \]

So at \(\theta =\dfrac{\pi }{4}\), the area \(A\) is maximized and the maximum area of the inscribed rectangle is \[ A\left( \dfrac{\pi }{4}\right) =4\sin \left( 2\cdot \frac{\pi }{4}\right) =4 \hbox{ square units} \]

The rectangle with the maximum area has \[ \hbox{length}\, 2x=4\cos \dfrac{\pi }{4}=2 \sqrt{2}\,\, \hbox{and height}\,\, y=2\, \sin \dfrac{\pi }{4} =\sqrt{2} \]