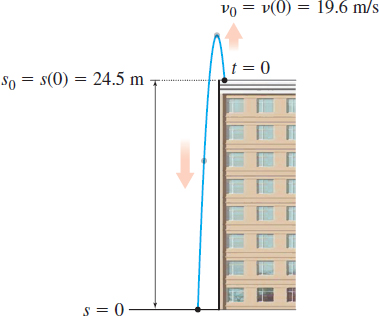
Solving a Problem Involving Free Fall

A rock is thrown straight up with an initial velocity of \(19.6\;{\rm m}/{\rm s}\) from the roof of a building \(24.5\;{\rm m}\) above ground level, as shown in Figure 64.

1. How long does it take the rock to reach its maximum altitude?
2. What is the maximum altitude of the rock?
3. If the rock misses the edge of the building on the way down and eventually strikes the ground, what is the total time the rock is in the air?

Solution To answer the questions, we need to find the velocity \(v=v(t)\) and the distance \(s=s(t)\) of the rock as functions of time. We begin measuring time when the rock is released. If \(s\) is the distance, in meters, of the rock from the ground, then since the rock is released at a height of \(24.5\;{\rm m}\), \(s_{0}=s(0)=24.5\;{\rm m}\).

The initial velocity of the rock is given as \(v_{0}=v(0)=19.6\;{\rm m}/{\rm s}\). If air resistance is ignored, the only force acting on the rock is gravity. Since the acceleration due to gravity is \(-9.8\;{\rm m}/{\rm s}^{2}\), the acceleration \(a\) of the rock is \[ a=\dfrac{{d\kern-1ptv}}{dt}=-9.8 \]

Solving the differential equation, we get \[ v(t)=-9.8t+v_{0} \]

Using the initial condition, \(v_{0}=v( 0) =19.6\;{\rm m}/{\rm s}\), the velocity of the rock at any time \(t\) is \[ v(t)=-9.8t+19.6 \]

Now we solve the differential equation \(\dfrac{ds}{dt}=v(t) =-9.8t+19.6\). Then \[ {s}(t)={-4.9t^{2}+19.6t+s_{0}} \]

Using the initial condition, \(s( 0) =24.5\;{\rm m}\), the distance \(s\) of the rock from the ground at any time \(t\) is \[ s(t)=-4.9t^{2}+19.6t+24.5 \]

Now we can answer the questions.

1. The rock reaches its maximum altitude when its velocity is \(0\). \begin{eqnarray*} v(t) &&= -9.8t+19.6=0 \\[6pt] t &&= 2 \end{eqnarray*} The rock reaches its maximum altitude at \(t=2\) seconds.
2. To obtain the maximum altitude, we evaluate \(s(2)\). The maximum altitude of the rock is \[ s(2)=-4.9( 2^2) +19.6( 2) +24.5=44.1{\rm m} \]
3. We find the total time the rock is in the air by solving \(s(t) =0\). \begin{eqnarray*} {\ -4.9t^{2}+19.6t+24.5} &&= 0 \\[1pt] {t^{2}-4t-5} &&= 0 \\[1pt] {(t-5)(t+1)} &&= 0 \\[1pt] t &&= 5\ \hbox{or}\quad t=-1 \end{eqnarray*}

336

The only meaningful solution is \(t=5\). The rock is in the air for \(5\) seconds.