Solving a Related Rate Problem

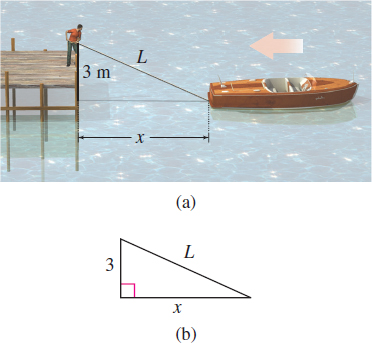
A person standing at the end of a pier is docking a boat by pulling a rope at the rate of \(2 \,{\rm m}/{\rm s}\). The end of the rope is \(3 \,{\rm m}\) above water level. See Figure 5(a). How fast is the boat approaching the base of the pier when \(5 \,{\rm m}\) of rope are left to pull in? (Assume the rope never sags, and that the rope is attached to the boat at water level.)

Solution

Step 1 Draw illustrations, like Figure 5, representing the problem. Label the sides of the triangle \(3\) and \(x\), and label the hypotenuse of the triangle \(L.\)

Step 2 \(x\) is the distance (in meters) from the boat to the base of the pier, \(L\) is the length of the rope (in meters), and the distance between the water level and the person's hand is \(3 \, {\rm m}\). Both \(x\) and \(L\) are changing with respect to time, so \(\dfrac{\textit{dx}}{\textit{dt}}\) is the rate at which the boat approaches the pier, and \(\dfrac{\textit{dL}}{ \textit{dt}}\) is the rate at which the rope is pulled in.

We are given \(\dfrac{\textit{dL}}{ \textit{dt}}=2 \,{\rm m}/{\rm s}\), and we seek \(\dfrac{\textit{dx}}{\textit{dt}}\) when \(L=5 \,{\rm m}\).

Step 3 The lengths \(3\), \(x\), and \(L\) are the sides of a right triangle and, by the Pythagorean Theorem, are related by the equation \begin{equation*} x^{2}+3^{2}=L^{2}\tag{2} \end{equation*}

Step 4 We differentiate both sides of equation (2) with respect to \(t.\) \[ \begin{eqnarray*} 2x\frac{\textit{dx}}{\textit{dt}} &=&2L\frac{\textit{dL}}{\textit{dt}} \\[3pt] \frac{\textit{dx}}{\textit{dt}} &=&\dfrac{L}{x}\frac{\textit{dL}}{\textit{dt}}\qquad \color{#0066A7}{{\hbox{ Solve for }\tfrac{\textit{dx}}{\textit{dt}}.}} \end{eqnarray*} \]

Step 5 When \(L=5\), we use equation (2) to find \(x=4\). Since \(\dfrac{\textit{dL}}{\textit{dt}}=2\), \[ \begin{eqnarray*} \frac{\textit{dx}}{\textit{dt}} &=&\dfrac{5}{4}(2) \qquad \color{#0066A7}{{\hbox{\({L=5},{x=4}, \tfrac{\textit{dL}}{\textit{dt}} =2\)}}} \\[3pt] \frac{\textit{dx}}{\textit{dt}} &=&2.5 \end{eqnarray*} \]

When \(5 \,{\rm m}\) of rope are left to be pulled in, the boat is approaching the pier at the rate of \(2.5 \,{\rm m}/{\rm s}\).