Identifying Maximum and Minimum Values and Local Extreme Values from the Graph of a Function

Figures 10, 11, 12, 13, 14 and 15 show the graphs of six different functions. For each function:

Continuity is discussed in Section 1.3, pp. 93-102.

  1. Find the domain.
  2. Determine where the function is continuous.
  3. Identify the absolute maximum value and the absolute minimum value, if they exist.
  4. Identify any local extreme values.

Solution

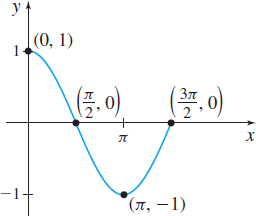
Figure 10 (a) Domain: \(\left[ 0,\dfrac{3\pi }{2}\right]\)
(b) Continuous on \(\left[ 0,\dfrac{3\pi }{2}\right]\)
(c) Absolute maximum value:
\(f( 0) =1\)
Absolute minimum value:
\(f( \pi ) =-1\)
(d) No local maximum value;
local minimum value: \(f( \pi ) =-1\)
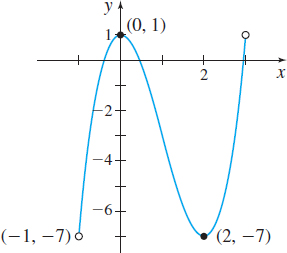
Figure 11 (a) Domain: \((-1,3)\)
(b) Continuous on \(( -1,3)\)
(c) Absolute maximum value:
\(f( 0) =1\)
Absolute minimum value:
\(f(2) =-7\)
(d) Local maximum value:
\(f( 0) =1\)
Local minimum value:
\(f(2) =-7\)
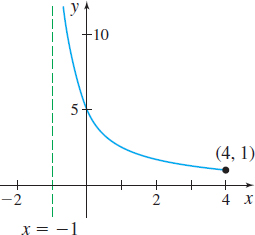
Figure 12 (a) Domain: \((-1,4]\)
(b) Continuous on \((-1,4]\)
(c) No absolute maximum value;
absolute minimum value:
\(f(4) =1\)
(d) No local maximum value;
no local minimum value
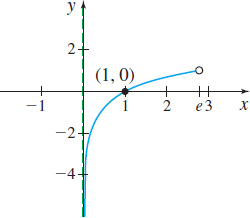
Figure 13 (a) Domain: \(( 0,e)\)
(b) Continuous on \(( 0,e)\)
(c) No absolute maximum value;
no absolute minimum value
(d) No local maximum value;
no local minimum value
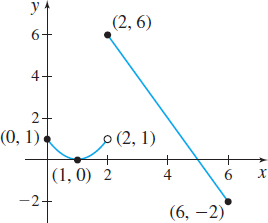
Figure 14 (a) Domain: \([ 0,6]\)
(b) Continuous on \([ 0,6]\) except
at \(x=2\)
(c)Absolute maximum value:
\(f(2) =6\)
Absolute minimum value:
\(f(6) =-2\)
(d) Local maximum value: \(f(2) =6\)
Local minimum value: \(f( 1) =0\)
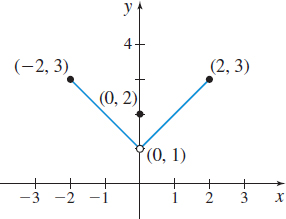
Figure 15 (a) Domain: \([ -2,2]\)
(b) Continuous on \([ -2,2]\) except at \(x=0\)
(c) Absolute maximum value:
\(f( -2) =3\), \(f(2) =3\)
No absolute minimum value
(d) Local maximum value: \(f( 0) =2\)
No local minimum value

265