Figure

EXAMPLE 4Finding Absolute Maximum and Minimum Values

Find the absolute maximum value and absolute minimum value of the function $f(x)=\left\{ {{ \begin{array}{@{}l@{\qquad}l@{\quad}l} {2x-1} & \text{if} & {0\leq x\leq 2} \\ {x^{2}-5x+9} & \text{if} & {2<x\leq 3} \end{array} }}\right.$

The function $f$ is continuous on the closed interval $[0,3]$ . (You should verify this.) To find the absolute maximum value and absolute minimum value, we follow the three-step procedure.

Step 1 Find the critical numbers in the open interval $(0,3)$ :

On the open interval

$(0, 2)$ :

$f(x)= 2x-1$ and

$f^\prime (x) =2$ . Since

$f^\prime (x) \neq 0$ on the interval

$(0, 2) ,$ there are no critical numbers in

$(0, 2)$ .

On the open interval

$(2, 3)$ :

$f(x)=x^{2}-5x+9$ and

$f^\prime (x) =2x - 5$ . Solving

$f^\prime (x) =2x-5=0$ , we find

$x=\dfrac{5}{2}$ . Since

$\dfrac{5}{2}$ is in the interval

$(2, 3)$ ,

$\dfrac{5}{2}$ is a critical number.

$x=2$ , the rule for

$f$ changes, so we investigate the one-sided limits of

$\dfrac{f(x) -f(2) }{x-2}.$

$\begin{eqnarray*} \lim\limits_{x\rightarrow 2^{-}}\dfrac{f(x) -f(2) }{ x-2} &=& \lim\limits_{x\rightarrow 2^{-}}\dfrac{(2x-1) -3}{x-2} =\lim\limits_{x\rightarrow 2^{-}}\dfrac{2x-4}{x-2}\\[3pt] &=&\lim\limits_{x\rightarrow 2^{-}}\dfrac{2(x-2) }{x-2}=2 \\[3pt] \lim\limits_{x\rightarrow 2^{+}}\dfrac{f(x) -f(2) }{ x-2} &=& \lim\limits_{x\rightarrow 2^{+}}\dfrac{(x^{2}-5x+9) -3}{x-2} =\lim\limits_{x\rightarrow 2^{+}}\dfrac{x^{2}-5x+6}{x-2}\\[3pt] &=&\lim\limits_{x \rightarrow 2^{+}}\dfrac{( x-2) (x-3) }{x-2} =\lim\limits_{x\rightarrow 2^{+}}(x-3) =-1 \end{eqnarray*}$

270

The one-sided limits are not equal, so the derivative does not exist at $2;$ $2$ is a critical number.

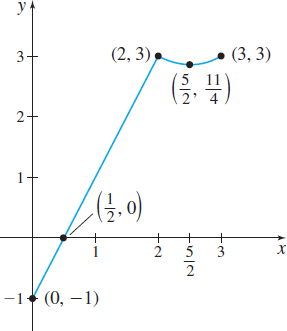
Figure 18

$\begin{equation*} f(x) =\left\{\begin{array}{lll} 2x-1&{\rm if}&0\leq x\leq 2\\[4pt] x^{2}-5x+9&{\rm if}&2 < x \leq 3 \end{array}\right. \end{equation*}$

Step 2 Evaluate $f$ at the critical numbers $\dfrac{5}{2}$ and $2$ and at the endpoints $0$ and $3$ .

$x$	${f(x)}$	${f(x)}$
$0$	$2\cdot 0-1$	$-1$	$\longleftarrow$ absolute minimum value
$2$	$2\cdot 2-1$	$3$	$\longleftarrow$ absolute maximum value
$\dfrac{5}{2}$	$\left( \dfrac{5}{2}\right) ^{\!\!2}-5\left( \dfrac{5}{2}\right) +9=\dfrac{25}{4}-\dfrac{25}{2}+9$	$\dfrac{11}{4}$
$3$	$3^{2}-5\cdot 3+9=9-15+9$	$3$	$\longleftarrow$ absolute maximum value

Step 3 The largest value $3$ is the absolute maximum value; the smallest value $-1$ is the absolute minimum value.