Find the $x$-intercepts of $f(x) = x^{2} - 5x + 6$, and show that $f^\prime (c) = 0$ for some number $c$ belonging to the interval formed by the two $x$-intercepts. Find $c$.

Solution At the $x$-intercepts, $f(x) = 0$. $$f(x)=x^{2}-5x+6=({x-2})({x-3})=0$$

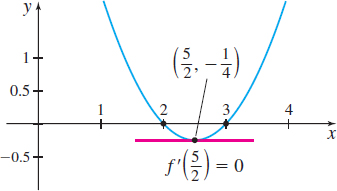
Figure 23 $f(x)=x^2-5x+6$

So, $x=2$ and $x=3$ are the $x$-intercepts of the graph of $f$, and $f(2) =$ $f(3) =0$.

Since $f$ is a polynomial, it is continuous on the closed interval $[2,3]$ formed by the $x$-intercepts and is differentiable on the open interval $(2,3)$. The three conditions of Rolle’s Theorem are satisfied, guaranteeing that there is a number $c$ in the open interval $(2,3)$ for which $f^\prime (c) = 0$. Since $f^\prime (x) = 2x-5,$ the number $c$ for which $f^\prime (x) =0$ is $c=\dfrac{5}{2}.$

See Figure 23 for the graph of $f$.