Verify that the function $f(x)=x^{3}-3x+5,$ $-1\leq x\leq 1$ satisfies the conditions of the Mean Value Theorem. Find the number(s) $c$ guaranteed by the Mean Value Theorem.

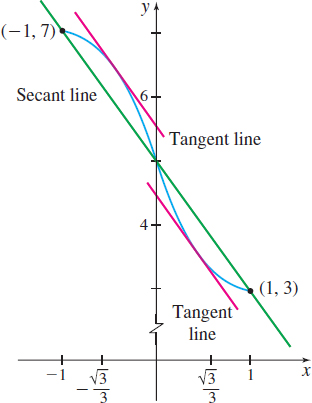
Figure 26 $f(x) = {x^3} - 3x + 5,$ $- 1 \le x \le 1$

Solution Since $f$ is a polynomial function, $f$ is continuous on the closed interval $[-1,1]$ and differentiable on the open interval $(-1,1)$. The conditions of the Mean Value Theorem are met. Now, $$f(-1) =7\qquad f(1) =3\qquad \hbox{ and }\qquad f^\prime (x) =3x^{2}-3$$

The number(s) $c$ in the open interval $(-1,1)$ guaranteed by the Mean Value Theorem satisfy the equation $$\begin{array}{l} \ \ \ \ f'\left( c \right) = \frac{{f\left( 1 \right) - f\left( { - 1} \right)}}{{1 - \left( { - 1} \right)}} \\ 3{c^2} - 3 = \frac{{3 - 7}}{{1 - \left( { - 1} \right)}} = \frac{{ - 4}}{2} = - 2 \\ \ \ \ \ \ \ 3{c^2} = 1 \\ \ \ \ \ \ \ \ \ \ \ c = \sqrt {\frac{1}{3}} = \frac{{\sqrt 3 }}{3}\,\,\,\,\,\,{\rm{or}}\,\,\,\,\,\,\,c = - \sqrt {\frac{1}{3}} = - \frac{{\sqrt 3 }}{3} \\ \end{array}$$

There are two numbers in the interval $(-1,1)$ that satisfy the Mean Value Theorem. See Figure 26.