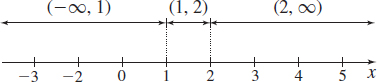Identifying Where a Function Is Increasing and Decreasing

Determine where the function \(f(x)=2x^{3}-9x^{2}+12x-5\) is increasing and where it is decreasing.

Solution The function \(f\) is a polynomial so \(f\) is continuous and differentiable at every real number. We find \(f^\prime .\) \[ f^\prime (x) =6x^{2}-18x+12=6({x-2})({x-1}) \]

The Increasing/Decreasing Function Test states that \(f\) is increasing on intervals where \(f^\prime (x) >0\) and that \(f\) is decreasing on intervals where \(f^\prime (x) <0\). We solve these inequalities by using the numbers \(1\) and \(2\) to form three intervals, as shown in Figure 27. Then we determine the sign of \(f^\prime (x)\) on each interval, as shown in Table 1.

TABLE 1
Interval Sign of \({x-1}\) Sign of \({x-2}\) Sign of \(f^\prime (x) = 6( x-2) ( x-1)\) Conclusion
\(( -\infty ,1)\) Negative \((-)\) Negative \((-)\) Positive \((+)\) \(f\) is increasing
\((1,2)\) Positive \((+)\) Negative \((-)\) Negative \((-)\) \(f\) is decreasing
\((2,\infty )\) Positive \((+)\) Positive \((+)\) Positive \((+)\) \(f\) is increasing

We conclude that \(f\) is increasing on the intervals \((-\infty ,1)\) and \((2,\infty)\), and \(f\) is decreasing on the interval \((1,2)\).