EXAMPLE 1Using the First Derivative Test to Find Local Extrema
Find the local extrema of f(x)=x4−4x3.
Solution Since f is a polynomial function, f is continuous and differentiable at every real number. We begin by finding the critical numbers of f. f′(x)=4x3−12x2=4x2(x−3)
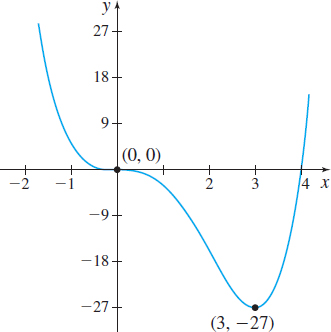
Figure 33 f(x)=x4−4x3
The critical numbers are 0 and 3. We use the critical numbers 0 and 3 to form three intervals, as shown in Figure 32. Then we determine where f is increasing and where it is decreasing by determining the sign of f′(x) in each interval. See Table 3.
| Interval | Sign of x2 | Sign of x−3 | Sign of f′(x)=4x2(x−3) | Conclusion |
|---|---|---|---|---|
| (−∞,0) | Positive (+) | Negative (−) | Negative (−) | f is decreasing |
| (0,3) | Positive (+) | Negative (−) | Negative (−) | f is decreasing |
| (3,∞) | Positive (+) | Positive (+) | Positive (+) | f is increasing |
Using the First Derivative Test, f has neither a local maximum nor a local minimum at 0, and f has a local minimum at 3. The local minimum value is f(3)=−27.
