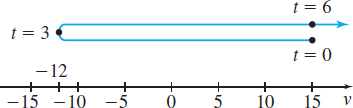Figure

EXAMPLE 3Using the First Derivative Test with Rectilinear Motion

Suppose the distance $s$ of an object from the origin at time $t\geq 0,$ in seconds, is given by $s=t^{3}-9t^{2}+15t+3$

(a) Determine the time intervals during which the object is moving to the right and to the left.
(b) When does the object reverse direction?
(c) When is the velocity of the object increasing and when is it decreasing?
(d) Draw a figure that illustrates the motion of the object.
(e) Draw a figure that illustrates the velocity of the object.

287

(a) To investigate the motion, we find the velocity $v$ . $v =\frac{\textit{ds}}{\textit{dt}}=3t^{2}-18t+15=3(t^{2}-6t+5)=3(t-1)(t-5)$

The critical numbers are $1$ and $5$ . We use Table 5 to describe the motion of the object.

TABLE 5

Time Interval	Sign of ${t-1}$	Sign of ${t-5}$	Velocity, ${v}$	Motion of the Object
$(0,1)$	Negative $(-)$	Negative $(-)$	Positive $(+)$	To the right
$(1,5)$	Positive $(+)$	Negative $(-)$	Negative $(-)$	To the left
$(5,\infty )$	Positive $(+)$	Positive $(+)$	Positive $(+)$	To the right

The object moves to the right for the first second and again after $5 \,{\rm seconds}$ . The object moves to the left on the interval $(1,5)$ .

(b) The object reverses direction at $t=1$ and $t=5$ .

(c) To determine when the velocity increases or decreases, we find the acceleration. $a=\frac{dv }{dt}=6t-18=6(t-3)$

Since $a<0$ on the interval $(0,3)$ , the velocity $v$ decreases for the first $3 \,{\rm seconds}$ . On the interval $(3,\infty), a>0$ , so the velocity $v$ increases from $3 \,{\rm seconds}$ onward.

(d) Figure 35 illustrates the motion of the object.

(e) Figure 36 illustrates the velocity of the object.

Figure 35

$s(t)=t^3-9t^2+15t+3$

Figure 36

$v(t)=3(t-1)(t-5)$