Solution (a) The first derivative of $f$ is $$f^\prime (x)=3x^{2}-12x+9=3( x-1) (x-3)$$

So, $1$ and $3$ are critical numbers of $f.$ Now,

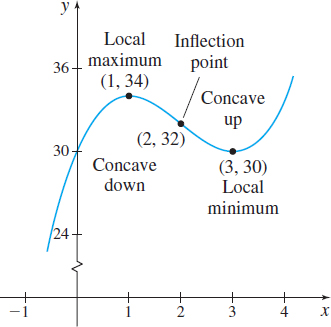
Figure 40 $f(x)=x^3-6x^2+9x+30$

So $f$ is increasing on $( -\infty ,1)$ and on $(3,\infty)$; $f$ is decreasing on $(1,3)$.

At $1,$ $f$ has a local maximum, and at $3$, $f$ has a local minimum. The local maximum value is $f( 1) = 34$; the local minimum value is $f(3) =30$.

(b) To determine concavity, we use the second derivative: $$f^{\prime \prime} (x)=6x-12= 6(x-2)$$

Now, we solve the inequalities $f^{\prime \prime} (x) <0$ and $f^{\prime \prime} (x) >0$ and use the Test for Concavity.