EXAMPLE 6Finding Inflection Points
Find the inflection points of f(x)=x5/3.
Solution We follow the steps for finding an inflection point.
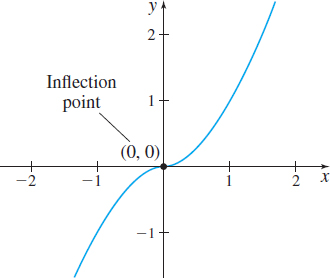
Figure 41 f(x)=x5/3
Step 1 The domain of f is all real numbers. The first and second derivatives of f are f′(x)=53x2/3f′′(x)=109x−1/3=109x1/3
The second derivative of f does not exist when x=0. So, (0,0) is a possible inflection point.
Step 2 Now use the Test for Concavity.
Step 3 Since the concavity of f changes at 0, we conclude that (0,0) is an inflection point of f.