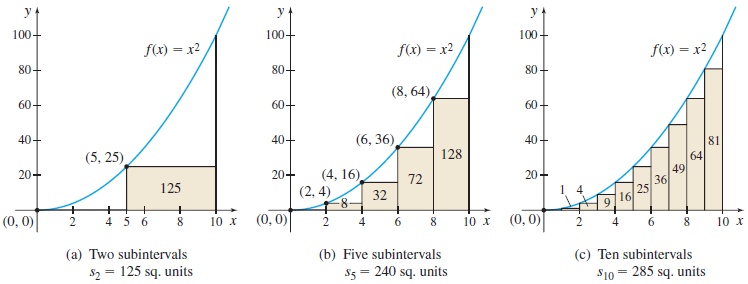
Approximating Area Using Lower Sums

Approximate the area \(A\) under the graph of \(f(x) = x^{2}\) from \(0\) to \(10\) by using lower sums \(s_{n}\) (rectangles that lie under the graph) for:

1. \(n = 2\) subintervals
2. \(n = 5\) subintervals
3. \(n = 10\) subintervals

Solution (a) For \(n=2\), we partition the closed interval \([0,10]\) into two subintervals \([0,5]\) and \([5,10]\), each of length \(\Delta x=\dfrac{10-0}{2}=5\). See Figure 9(a). To compute \(s_{2}\), we need to know where \(f\) attains its minimum value in each subinterval. Since \(f\) is an increasing function, the absolute minimum is attained at the left endpoint of each subinterval. So, for \(n=2,\) the minimum of \(f\) on \([0,5] \) occurs at \(0\) and the minimum of \(f\) on \([5,10] \) occurs at 5. The lower sum \(s_{2}\) is

347

\[ s_{2}=\sum\limits_{i=1}^{2}~f(c_{i})\Delta x=\Delta x\sum\limits_{i=1}^{2}f(c_{i}) \underset{\underset{\underset{\color{#0066A7}{f\left(c_{1}\right) =f\left( 0\right);f\left( c_{2}\right) =f\left(5\right)}}{\color{#0066A7}{\Delta x=5}}}{\color{#0066A7}{\uparrow}}}{=}5\,\left[ ~f(0)+f(5)\right] \underset{\underset{\underset{\color{#0066A7}{f(5)=25}}{\color{#0066A7}{f(0)=0}}}{\color{#0066A7}{\uparrow}}}{=}5(0+25)=125 \]

(b) For \(n=5\), partition the interval \([0,10]\) into five subintervals \([0,2] ,\) \([2,4] ,\) \([4,6] , \) \([6,8] ,\) \([8,10]\), each of length \(\Delta x = \dfrac{10-0}{5}=2\). See Figure 9(b). The lower sum \(s_{5}\) is \[ \begin{eqnarray*} s_{5} &=&\sum\limits_{i=1}^{5} f(c_{i})\Delta x=\Delta x\sum\limits_{i=1}^{5}f(c_{i})=2 [ f(0)+f(2)+f(4) +f(6)+f(8)] \\ &=&2(0+4+16+36+64)=240 \end{eqnarray*} \]

(c) For \(n=10\), partition \([0,10]\) into \(10\) subintervals, each of length \(\Delta x=\dfrac{10-0}{10}=1\). See Figure 9(c). The lower sum \(s_{10}\) is \[ \begin{eqnarray*} s_{10} &=&\sum\limits_{i=1}^{10} f(c_{i})\Delta x=\Delta x\sum\limits_{i=1}^{10}f(c_{i})=1[ f(0)+f(1)+f(2)+\cdots +f(9) ] \\ &=&0+1+4+9+16+25+36+49+64+81=285 \end{eqnarray*} \]