Forming Riemann Sums

For the function \(f(x) =x^{2}-3,\) \(0\leq x\leq 6,\) partition the interval \([0,6] \) into 4 subintervals \([0,1]\), \([1,2]\), \([2,4]\), \([4,6]\) and form the Riemann sum for which

1. \(u_{i}\) is the left endpoint of each subinterval.
2. \(u_{i}\) is the midpoint of each subinterval.

Solution In forming Riemann sums \(\sum\limits_{i=1}^{n}f(u_{i}) \Delta x_{i}\), \(n\) is the number of subintervals in the partition, \(f(u_{i}) \) is the value of \(f\) at the number \(u_{i}\) chosen in the \(i\)th subinterval, and \(\Delta x_{i}\) is the length of the \(i\)th subinterval.

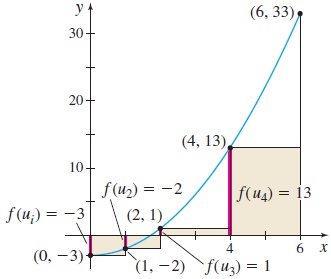
(a) Figure 16 shows the graph of \(f,\) the partition of the interval \([0,6] \) into the 4 subintervals, and values of \(f(u_{i}) \) at the left endpoint of each subinterval, namely, \[ \begin{array}{rcl@{\qquad}crcl} f(u_{1}) &=& f(0) =-3 & f(u_{2}) &=&f(1) =-2\\ f(u_{3}) &=& f(2) =1 & f(u_{4}) &=& f(4) = 13 \end{array} \]

The 4 subintervals have length \[ \Delta x_{1}=1-0=1 \qquad \Delta x_{2}=2-1=1 \qquad \Delta x_{3}=4-2=2 \qquad \Delta x_{4}=6-4=2 \]

The Riemann sum is formed by adding the products \(f(u_{i}) \Delta x_{i}\) for \(i=1,2,3,4\). \[ \sum\limits_{i=1}^{4} f(u_{i}) \Delta x_{i}=-3\cdot 1 + (-2) \cdot 1+1\cdot 2 + 13 \cdot 2=23 \]

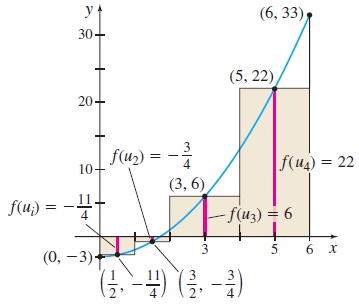
(b) See Figure 17. If \(u_{i}\) is chosen as the midpoint of each subinterval, then the value of \(f(u_{i}) \) at the midpoint of each subinterval is \[ \begin{array}{rcl@{\qquad}crcl} f(u_{1}) &=& f\left(\dfrac{1}{2}\right) =-\dfrac{11}{4} & f(u_{2}) &=&f\left( \dfrac{3}{2}\right) =-\dfrac{3}{4}\\ f(u_{3}) &=&f (3) =6 & f(u_{4}) &=& f(5) = 22 \end{array} \]

The Riemann sum formed by adding the products \(f(u_{i}) \Delta x_{i}\) for \(i=1,2,3,4\) is \[ \sum\limits_{i=1}^{4}f(u_{i}) \Delta x_{i}=-\dfrac{11}{4} \cdot 1 + \left(-\dfrac{3}{4}\right) \cdot 1 + 6 \cdot 2 + 22 \cdot 2 =\dfrac{105}{2}=52.5 \]