Determine if each definite integral can be interpreted as an area. If it can, describe the area; if it cannot, explain why.

Solution (a) See Figure 19. Since $\cos x\lt0$ on the interval $\left(\dfrac{\pi }{2},\dfrac{3\pi}{4}\right],$ the integral $\int_{0}^{3\pi /4}\cos x\,dx$ cannot be interpreted as area.

(b) See Figure 20. Since $\vert x-4\vert \geq 0$ on the interval $[2,10]$, the integral $\int_{2}^{10}\vert x-4\vert \,dx$ can be interpreted as the area enclosed by the graph of $y=\vert x-4\vert$, the $x$-axis, and the lines $x=2$ and $x=10.$

359

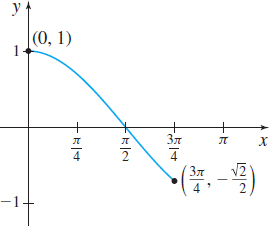
Figure 19 $f(x) = \cos x, 0 \leq x \leq \dfrac{3\pi}{4}$

Figure 20 $f(x) = \vert x- 4 \vert, 2 \leq x \leq 10$