Find the area $A$ under the graph of

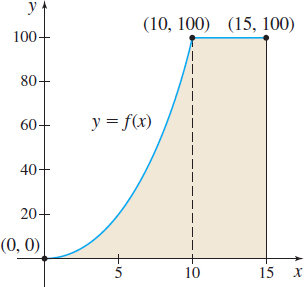
Figure 25 $A=\int^{15}_0 f(x)\, dx$

$$f(x) =\left\{ \begin{array}{c@{ }c@{ }ccc} x^{2} & \hbox{if} & 0 & \leq x &\lt10 \\ 100 & \hbox{if} & 10 &\leq x & \leq 15 \end{array} \right.$$

from $0$ to $15.$

Solution See Figure 25. Since $f$ is nonnegative on the closed interval $[0,15] ,$ then $\int_{0}^{15}f(x)\, dx$ equals the area $A$ under the graph of $f$ from $0$ to $15.$ Since $f$ is continuous on $[0,15],$ $$\begin{eqnarray*} \int_{0}^{15}f(x)\, dx &=& \int_{0}^{10}f(x)\, dx+\int_{10}^{15}f(x)\, dx=\int_{0}^{10}x^{2}dx+\int_{10}^{15}100\,dx \\[4.5pt] &=& \left[\dfrac{x^{3}}{3}\right] _{0}^{10}+ \Big[100x\Big] _{10}^{15}=\dfrac{1000}{3}+500=\dfrac{2500}{3} \end{eqnarray*}$$

The area under the graph of $f$ is approximately 833.33 square units.