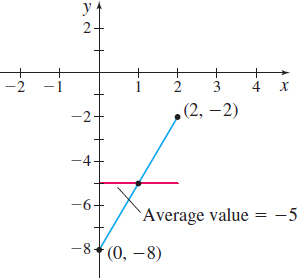
Figure 30 $f(x) = 3x-8,0 \leq x \leq 2$

Find the average value of $f(x)=3x-8$ on the closed interval $[0,2] .$

Solution The average value of $f(x)=3x-8$ on the closed interval $[0,2]$ is given by $$\begin{eqnarray*} \bar{y} &=&\dfrac{1}{b-a}\int_{a}^{b}f(x)\,dx=\dfrac{1}{2-0}{\int_{0}^{2}}(3x-8) dx\\ &=& \dfrac{1}{2}\left[\dfrac{3x^{2}}{2}-8x \right] _{0}^{2} =\dfrac{1}{2}(6-16) =-5 \end{eqnarray*}$$

The average value of $f$ on $[0,2]$ is $\bar{y}=-5.$