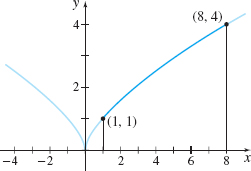
Find the arc length of the graph of the function $f(x) =x^{2/3}$ from $x=1$ to $x=8$.

Solution We begin by graphing $f(x) =x^{2/3}$. See Figure 50.

Figure 50 $f(x) =x^{2/3}, 1 \leq x \leq 8$.

441

The derivative of $f(x)=x^{2/3}$ is $f' (x)=\dfrac{2}{3}x^{-1/3}=\dfrac{2}{3x^{1/3}}$. Notice that $f'$ is not continuous at $0$. However, since $f'$ is continuous on an interval containing $1$ and $8$ (use $\left[ \dfrac{1}{2},9\right]$, for example, which avoids $0)$, we use the arc length formula (1). The arc length $s$ from $x=1$ to $x=8$ is $$\begin{eqnarray*} s&=&\int_{1}^{8}\sqrt{1+\left[ f' (x) \right] ^{2}} ~{\it dx}=\int_{1}^{8}\sqrt{1+\left( \frac{2}{3x^{1/3}}\right) ^{2}} ~{\it dx}=\int_{1}^{8}\sqrt{1+\frac{4}{9x^{2/3}}}~{\it dx} \\[5pt] &=&\int_{1}^{8}\sqrt{\frac{9x^{2/3}+4}{9x^{2/3}}}~{\it dx} \underset{\underset{\underset{\color{#0066A7}{\hbox{so \(\sqrt{x^{2/3}} =x^{1/3}\)}}}{\color{#0066A7}{\hbox{\(x>0\) on \([1,8]\),}}}} {\color{#0066A7}{\uparrow }}} {=} {\frac{1}{3}} \int_{1}^{8}\Big( x^{-1/3}\sqrt{9x^{2/3}+4}\Big) ~{\it dx}\\[-9pt] \end{eqnarray*}$$

We use the substitution $u=9x^{2/3}+4.$ Then ${\it du}=6x^{-1/3}{\it dx}$ and, $x^{-1/3}{\it dx}=\dfrac{{\it du}}{6}$. The limits of integration change to $u=13$ when $x=1$, and to $u=40$ when $x=8$. Then $$\begin{eqnarray*} s&=&\dfrac{1}{3} \displaystyle \int_{1}^{8}\Big[ x^{-1/3}\sqrt{~9x^{2/3}+4}\Big] ~{\it dx}= \dfrac{1}{3}\displaystyle \int_{13}^{40}\sqrt{~u}~\dfrac{{\it du}}{6}= \dfrac{1}{18} \left[\dfrac{u^{3/2}}{\dfrac{3}{2}}\right] _{13}^{40}\\[5pt] &=&\dfrac{1}{27}\big( 80\sqrt{10}-13\sqrt{13}\big) \end{eqnarray*}$$