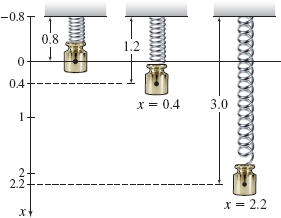
Analyzing a Spring Force

Suppose a spring in equilibrium is \(0.8\textrm{ m}\) long and a spring force of \(2\textrm{ N}\) stretches the spring to a length of \(1.2\textrm{ m}.\)

1. Find the spring constant \(k\) and the spring force \(F\).
2. What spring force is required to stretch the spring to a length of \(3\textrm{ m}\)?
3. How much work is done by the spring force in stretching it from equilibrium to \(3\textrm{ m}\)?

Solution We position an axis parallel to the spring and place the origin at the free end of the spring in equilibrium, as in Figure 56.

1. When the spring is stretched to a length of \(1.2\textrm{ m}\), then \(x=0.4\). Using Hooke's Law, we get \begin{eqnarray*} -2 &=&-k( 0.4) \qquad\quad {\color{#0066A7}{\hbox{Hooke's law:} F(x)=-kx; F=-2; x=0.4}} \\[4pt] k &=&\dfrac{2}{0.4}=5\textrm{N}/\textrm{ m} \end{eqnarray*} The spring constant is \(k=5\). The spring force \(F\) is \(F=-kx=-5x.\)
2. The spring force \(F\) required to stretch the spring to a length of \(3\textrm{ m}\), that is, a distance \(x=3-0.8=2.2\textrm{ m}\) from equilibrium, is \[ F=-5x=( -5) ( 2.2) =-11\textrm{ N} \]
3. The work \(W\) done by the spring force \(F\) when stretching the spring from equilibrium \((x=0)\) to \(x=2.2\) is \[ \begin{eqnarray*} W&=&\int_{0}^{2.2}F(x) {\it dx} \underset{\underset{\color{#0066A7}{\hbox{\(F(x) = -5x\)}}}{\color{#0066A7}{\uparrow }}} {=} -5\int_{0}^{2.2}x\,{\it dx}= -5\left[ \dfrac{x^{2}}{2} \right] _{0}^{2.2}=-\dfrac{5}{2}(4.84)=-12.1\textrm{ J} \nonumber\\[-11pt] && \end{eqnarray*} \]