Finding the Work Required to Pump Water from a Tank

A water tank in the shape of a hemisphere of radius \(2\textrm{ m}\) is full of water. How much work is required to pump all the water to a level \(3\textrm{ m}\) above the tank?

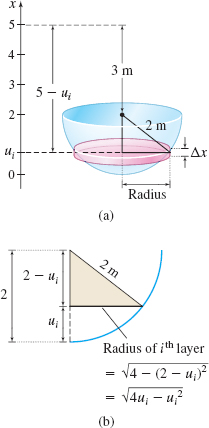
Solution We position an \(x\)-axis so the bottom of the tank is at \(x=0\) and the top of the tank is at \(x=2\), as illustrated in Figure 59(a).*

The work required to pump the water to a level \(3\textrm{ m}\) above the top of the tank depends on the weight of the water and its distance from a level \(3\textrm{ m}\) above the tank. The water fills the container from \(x=0\) to \(x=2.\)

Partition the interval \([ 0, 2]\) into \(n\) subintervals, each of width \(\Delta x=\dfrac{2}{n}\), and choose a number \(u_{i}\) in each subinterval. Now think of the water in the tank as \(n\) circular layers, each of thickness \(\Delta x\). As Figure 59(b) illustrates, the radius of the circular layer \(u_{i}\) meters from the bottom of the tank is \(\sqrt{4u_{i}-u_{i}^{2}}\). Then \begin{align*} \hbox{Volume }V_{i}\hbox{ of }i{\hbox{th }}\hbox{layer}&=\pi (\hbox{Radius} )^{2}\hbox{(Thickness)}\\[5pt] &=\pi \Big( \sqrt{4u_{i}-u_{i}^{2}}\Big) ^{2}\Delta x =\pi \big( 4u_{i}-u_{i}^{2}\big) \Delta x \end{align*}

The density of water is \(\rho =1000\textrm{ kg} \textrm{/m}^{3},\) so \begin{align*} \hbox{Weight of }i{\hbox{th }}\hbox{layer} & =\rho gV_{i}=(1000) ( 9.8) \pi \big(4u_{i}-u_{i}^{2}\big)\Delta x\, \\ \hbox{Distance }i{\hbox{th}}\hbox{ layer is lifted} & =5-u_{i} \\ \hbox{Work done in lifting }i{\hbox{th}}\hbox{ layer} & =9800\,\pi \big(4u_{i}-u_{i}^{2}\big)(5-u_{i})~\Delta x \end{align*}

The work \(W\) required to lift all the water from the tank to a level 3 m above the top of the tank is given by \begin{eqnarray*} W &=&\int_{0}^{2}9800~\pi (4x-x^{2})(5-x)~{\it dx}=9800\pi \displaystyle \int_{0}^{2}(x^{3}-9x^{2}+20x) ~{\it dx} \notag \\[5pt] &=&9800~\pi \left[ \dfrac{x^{4}}{4}-3x^{3}+10x^{2}\right] _{0}^{2}=196{,}000\pi \approx 615{,}752~\textrm{J} \end{eqnarray*}