Finding Hydrostatic Force

A trough, whose cross section is a trapezoid, measures 2 m across at the bottom and 4 m across at the top, and is 2 m deep. If the trough is filled with a liquid of mass density \(\rho\), what is the force due to hydrostatic pressure on one end of the trough?

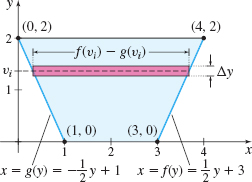
Solution We position the trough in a rectangular coordinate system, as shown in Figure 62.

The sides of the end of the trough are lines that pass through the points \( (0,2),\) \((1,0)\) and the points \((3,0),\) \((4,2)\), respectively. The equations of these lines are \begin{equation*} y-2=\dfrac{0-2}{1-0}(x-0)=-2x\qquad\hbox{or equivalently}\qquad x=g(y)=-\dfrac{1}{2}y+1 \end{equation*}

and \begin{equation*} y-0=\dfrac{2-0}{4-3}(x-3)=2x-6\qquad\hbox{or equivalently}\qquad x=f(y)=\dfrac{1}{2}y+3 \end{equation*}

Then the hydrostatic force on the \(i\)th interval of the trough is \begin{equation*} F_{i}=\,\underset{\color{#0066A7}{\hbox{Weight}}}{\underbrace{\rho \cdot g\,}}\underset{\color{#0066A7}{\hbox{ Depth}}}{\underbrace{( H-v_{i}) }\,}\underset{\color{#0066A7}{\hbox{Area}}}{ \underbrace{[ f( v_{i}) -g( v_{i}) ] \Delta y}}\underset{\color{#0066A7}{\hbox{$H=2$}}}{\underset{\color{#0066A7}{\uparrow }}{=}}\rho g( 2-v_{i}) [ f( v_{i}) -g( v_{i}) ] \Delta y \end{equation*}

The liquid fills the trough from \(y=0\) to \(y=2,\) so the hydrostatic force \(F\) due to the pressure of the liquid on an end of the trough is \begin{eqnarray*} F &=&\int_{0}^{2}\rho g(2-y)[f(y)-g(y)] ~{\it dy}\\[5pt] &=&\int_{0}^{2}\rho g(2-y)\left[ \left( \dfrac{1}{2}y+3\right) -\left( -\dfrac{1}{2}y+1\right) \right] {\it dy}=\rho g\int_{0}^{2}(2-y)(y+2)~{\it dy} \notag \\[5pt] &=&\rho g\int_{0}^{2}(-y^{2}+4)~{\it dy}=\rho g\left[ -\dfrac{y^{3}}{3}+4y\right] _{0}^{2}=\rho g\!\left( -\dfrac{8}{3}+8\right) =\dfrac{16}{3}\rho g\hbox{ } \textrm{ N} \end{eqnarray*}