A cylindrical sewer pipe of radius 2 m is half full of water. A gate used to seal off the sewer is placed perpendicular to the pipe opening. Find the hydrostatic force exerted on one side of the gate.

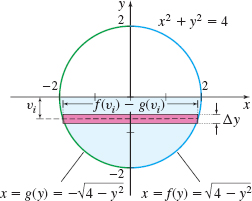
Solution We position a cross section of the pipe (a circle) so its center is at the origin. See Figure 63.

Figure 63

The equation of the circle with center at $(0,0)$ and radius $2$ is $x^{2}+y^{2}=4$. Then $$x=g(y)=-\sqrt{4-y^{2}}\qquad \hbox{and }\qquad x=f(y)=\sqrt{4-y^{2}}$$

The height of the water is at $H=0$. Since the water fills the cylinder from $y=-2$ to $y=0,$ the hydrostatic force $F$ exerted on one side of the gate by the pressure of the water is $$\begin{array}{rcl@{\qquad}l} F &=&\int_{c}^{d}\rho g( {H-y}) [ f(y)-g(y)] ~{\it dy} & \\[3pt] &=&\int_{-2}^{0}\rho g(0-y)\big[ \sqrt{4-y^{2}}-\big( -\!\sqrt{4-y^{2}}\big) \big] ~{\it dy} &\color{#0066A7}{H=0; c=-2; d=0.} \\ &=&9800\int_{-2}^{0}-2y\sqrt{4-y^{2}}~{\it dy} &\color{#0066A7}{\rho =1000\hbox{ kg}/\hbox{m}^{3}; g=9.8\ \hbox{ m}/\hbox{s}^{2}.} \\ &=&9800\int_{0}^{4}\sqrt{u}~{\it du}=9800\left[ \frac{2u^{3/2}}{3}\right]_{0}^{4} &\color{#0066A7}{\hbox{Let \(u=4-y^{2} \); }} \\ &&&\color{#0066A7}{\hbox{then \(du=-2y~{dy} \).}}\\ &&&\color{#0066A7}{\hbox{When \(y=-2 \), then \(u=0 \);}} \\ &&&\color{#0066A7}{\hbox{when \(y=0 \), then \(u=4 \).}}\\[-3pc] \\ &=&9800\left( \dfrac{16}{3}\right) \approx 52{,}267 {N} \end{array}$$