Find the centroid of the homogeneous lamina bounded by the graph of $f(x)=x^{2},$ the $x$-axis, and the line $x=1$.

Solution The lamina is shown in Figure 71.

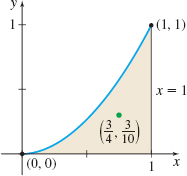
Figure 71 $f(x)=x^{2}$, $0\leq x\leq 1$.

The area $A$ of the lamina is $$\begin{equation*} A=\int_{0}^{1}x\,^{2}{\it dx}=\left[ \dfrac{x^{3}}{3}\right] _{0}^{1}=\dfrac{1}{3} \end{equation*}$$

Using formulas (2), the centroid of the lamina is $$\begin{equation*} \bar{x} = \dfrac{1}{A}\int_{0}^{1}xf(x)~{\it dx}=\dfrac{1}{\dfrac{1}{3}} \displaystyle \int_{0}^{1}~x\cdot x^{2}\,{\it dx}=3\displaystyle \int_{0}^{1}x^{3}\,{\it dx}=3\left[ \dfrac{x^{4}}{4}\right] _{0}^{1}=\dfrac{3}{4} \\[4pt] \bar{y} = \dfrac{1}{2A}\displaystyle \int_{0}^{1}[f(x)] ^{2}\,{\it dx}=\dfrac{1}{\dfrac{2}{3}}\displaystyle \int_{0}^{1}( x^{2}) ^{2}\,{\it dx}=\dfrac{3}{2} \displaystyle \int_{0}^{1}x^{4}\,{\it dx}=\dfrac{3}{2}\left[ \dfrac{x^{5}}{5}\right] _{0}^{1}=\dfrac{3}{10} \end{equation*}$$

The centroid of the lamina is $\left( \dfrac{3}{4},\dfrac{3}{10}\right) .$