Finding the Centroid of a Homogeneous Lamina

Find the centroid of one-quarter of a circular plate of radius \(R\).

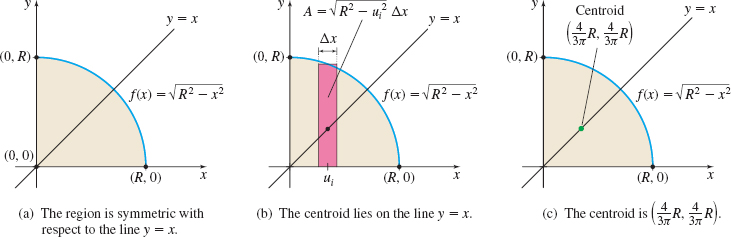
Solution We place the quarter-circle in the first quadrant, as shown in Figure 72(a). The equation of the quarter circle can be expressed as \(f(x)= \sqrt{R^{2}-x^{2}}\), where \(0\leq x\leq R\).

If you guessed that because the quarter of the circular plate is symmetric with respect to the line \(y=x\), the centroid will lie on this line, you are correct. See Figure 72(b). So, \(\bar{x}=\bar{y} \). The area \(A\) of the quarter circular region is \(A=\dfrac{\pi R^{2}}{4}\). \begin{equation*} \begin{array}{lll} \bar{x}=\dfrac{1}{A}\displaystyle \int_{a}^{b}\left[ xf(x)\right] {\it dx}=\dfrac{1}{A} \int_{0}^{R}x\sqrt{R^{2}-x^{2}}{\it dx}\\ \bar{y}=\dfrac{1}{2A}\displaystyle \int_{a}^{b}\left[ f(x)\right] ^{2}{\it dx}=\dfrac{1}{2A} \int_{0}^{R}\left( R^{2}-x^{2}\right) {\it dx} \end{array} \end{equation*}

463

Since \(\bar{x}=\bar{y},\) and \(\bar{y}\) is easier to find, we evaluate \(\bar{y }.\) \begin{equation*} \bar{x}=\bar{y}=\dfrac{1}{2A}\int_{0}^{R}( R^{2}-x^{2})\, {\it dx}=\dfrac{ 1}{2\left( \dfrac{\pi R^{2}}{4}\right) }\left[ R^{2}x-\dfrac{x^{3}}{3}\right] _{0}^{R}=\dfrac{2}{\pi R^{2}}\left( \dfrac{2}{3}R^{3}\right) =\dfrac{4}{3\pi }R \end{equation*}

The centroid of the lamina, as shown in Figure 72(c), is \(\left( \bar{x},\bar{y}\right) =\left( \dfrac{4% }{3\pi }R,\dfrac{4}{3\pi }R\right) \).