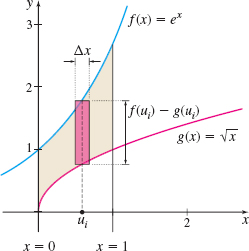
Finding the Area Between the Graphs of Two Functions

Find the area of the region enclosed by the graphs of \(f(x) =e^{x}\) and \(g(x) =\sqrt{x}\) and the lines \(x=0\) and \(x=1\).

Solution We begin by graphing the two functions and identifying the area \(A\) to be found. See Figure 3.

From the graph, we see that \(f(x) \geq g(x)\) on the interval \([0,1]\). Then, using the definition of area, we have \begin{eqnarray*} A &=&\int_{a}^{b}[f(x)-g(x)]~{\it dx}=\int_{0}^{1}( e^{x}-\sqrt{x}) ~{\it dx}\\[2pt] &=&\int_{0}^{1}e^{x}~{\it dx}-\int_{0}^{1}x^{1/2}~{\it dx}=\big[ e^{x}\big] _{0}^{1}-\left[ \dfrac{x^{3/2}}{\dfrac{3}{2}}\right] _{0}^{1} \\[5pt] &=&( e^{1}-e^{0}) -\dfrac{2}{3}( 1-0) =e-1-\dfrac{2}{3}=e-\dfrac{5}{3} \hbox{ square units} \end{eqnarray*}