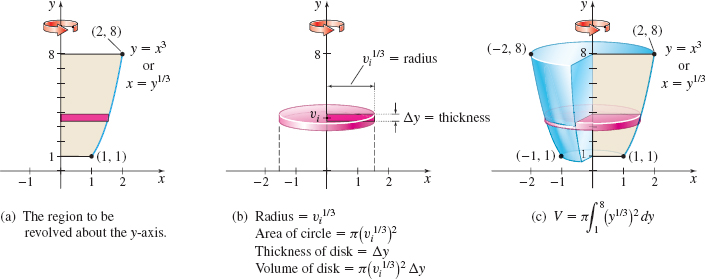
Using the Disk Method: Revolving About the \(y\)-Axis

Use the disk method to find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=x^{3}\), the \(y\)-axis, and the lines \(y=1\) and \(y=8\) about the \(y\)-axis.

Solution Figure 20(a) shows the region to be revolved. Since the solid is formed by revolving the region about the \(y\)-axis, we write \(y=x^{3}\) as \(x=\sqrt[3]{y}=y^{1/3}\). Figure 20(b) illustrates a typical disk, and Figure 20(c) shows the solid of revolution. Using the disk method, the volume \(V\) of the solid of revolution is \begin{eqnarray*} V&=&\pi \int_{1}^{8}[ y^{1/3}] ^{2}~{\it dy}=\pi \int_{1}^{8}y^{2/3}~{\it dy}=\pi \left[ \dfrac{y^{5/3}}{\dfrac{5}{3}}\right]_{1}^{8}\\[8pt] &=&\dfrac{3\pi }{5}(32-1)=\dfrac{93}{5}\pi \hbox{ cubic units} \end{eqnarray*}