Finding the Volume of a Solid: Revolving About the \(y\)-Axis

Find the volume \(V\) of the solid generated by revolving the region bounded by the graphs of \(f(x) =x^{2}+2x\), the \(x\)-axis, and the line \(x=1\) about the \(y\)-axis.

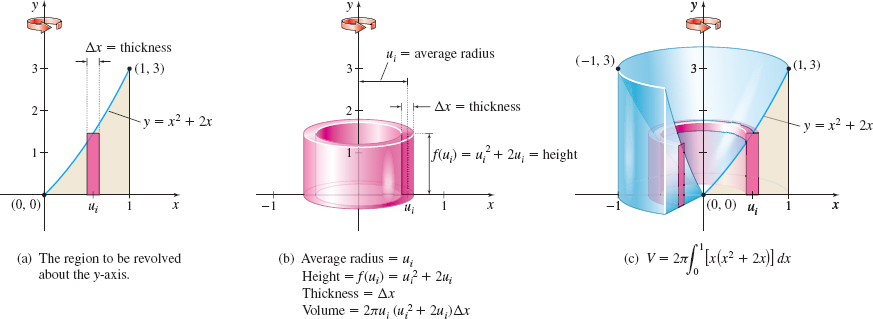
Solution Using the shell method: In the shell method, when a region is revolved about the \(y\)-axis, we partition the \(x\)-axis and use vertical shells. Figure 31(a) illustrates the region to be revolved and a typical rectangle of height \(f(u_{i})\) and thickness \(\Delta x\) that will become a shell with average radius \(u_{i}\) when it is revolved about the \(y\)-axis. The volume of a typical shell is \(V_{i}=2\pi\) (Average radius)(Height)(Thickness) \(=2\pi u_{i} f(u_{i})\Delta x\), as shown in Figure 31(b). Figure 31(c) illustrates the solid of revolution. The volume \(V\) of the solid of revolution is \begin{eqnarray*} V&=&2\pi \int_{0}^{1}xf(x) {\it dx}=2\pi \int_{0}^{1}[ x(x^{2}+2x) ] ~{\it dx}=2\pi \int_{0}^{1}(x^{3}+2x^{2})~{\it dx}\\[4pt] &=&2\pi\! \left[ \dfrac{x^{4}}{4}+ \dfrac{2x^{3}}{3}\right] _{0}^{1}=\dfrac{11\pi }{6}\hbox{ cubic units} \end{eqnarray*}

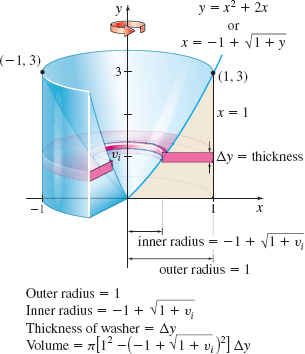
Using the washer method: Using the washer method, a revolution about the \(y\)-axis requires integration with respect to \(y\). This means we need to find the inverse function of \(y=f(x)\). We treat \(x^{2}+2x-y=0\) as a quadratic equation in the variable \(x\) and use the quadratic formula with \(a=1, b=2\), and \(c=-y\) to obtain \(x=g(y)=-1\pm \sqrt{1+y}\). Since \(x\geq 0\), we use the \(+\) sign.

See Figure 32. The volume of a typical washer is \[ V_{i}=\pi [ (\hbox{Outer radius}) ^{2}-( \hbox{Inner radius}) ^{2}]\times (\hbox{Thickness}). \]

The volume \(V\) of the solid of revolution is \begin{eqnarray*} V &=&\pi \int_{0}^{3} [ 1^{2}- ( -1+\sqrt{1+y}) ^{2}] ~{\it dy}=\pi \int_{0}^{3} [ 1- ( 1-2\sqrt{1+y}+1+y) ] ~{\it dy}\\[4pt] &=&\pi \int_{0}^{3} [ 2\sqrt{1+y}-1-y]\, {\it dy} =\pi \int_{0}^{3} ( 2\sqrt{1+y}) {\it dy}-\pi \int_{0}^{3}(1+y)~{\it dy} \end{eqnarray*}

*This topic is discussed in detail in an article by Charles A. Cable (February 1984), “The Disk and Shell Method,” American Mathematical Monthly, 91(2), 139.

427

The two integrals are found as follows:

\( \pi \displaystyle \int_{0}^{3}(2\sqrt{1+y})~ {\it dy} \underset{\underset{\underset{\color{#0066A7}{\hbox{then \({du}={dy}\)}}}{\color{#0066A7}{\hbox{Let \(u=1+y\);}}}}{\color{#0066A7}{\uparrow }}} {=} 2\pi \displaystyle \int_{1}^{4}u^{1/2}\ {\it du}=2\pi \left[ \dfrac{u^{3/2}}{\dfrac{3}{2}}\right]_{1}^{4}=\dfrac{28\pi }{3} \)

\(\pi \displaystyle \int_{0}^{3}(1+y)~{\it dy}=\pi \left[ y+\dfrac{y^{2}}{2}\right] _{0}^{3}= \dfrac{15\pi }{2}\)

The volume \(V\) is \[ V=\frac{28\pi }{3}-\frac{15\pi }{2}=\frac{11\pi }{6}\hbox{ cubic units} \]